- School of Natural and Environmental Sciences, Newcastle University, Newcastle upon Tyne, United Kingdom
Future energy systems with a greater share of renewable energy will require long-duration energy storage (LDES) to optimise the integration of renewable sources and hydrogen is one energy vector that could be utilised for this. Grid-scale underground storage of natural gas (methane) is already in operation in solution-mined salt caverns, where individual cavern capacities are ∼0.025–0.275 TWh. While salt caverns have traditionally been restricted to being developed onshore, in some offshore locations, such as the UK Continental Shelf, there are extensive evaporites that have the potential for storage development. Capacity estimates for offshore areas typically rely on generalised regional geological interpretations; they frequently do not incorporate site-specific structural and lithological heterogeneities, they use static cavern geometries and may use methodologies that are deterministic and not repeatable. We have developed a stochastic method for identifying potential salt cavern locations and estimating conceptual cluster storage capacity. The workflow incorporates principle geomechanical constraints on cavern development, captures limitations from internal evaporite heterogeneities, and uses the ideal gas law to calculate the volumetric capacity. The workflow accommodates either fixed cavern geometries or geometries that vary depending on the thickness of the salt. By using a stochastic method, we quantify the uncertainties in storage capacity estimates and cavern placement over defined regions of interest. The workflow is easily adaptable allowing users to consider multiple geological models or to evaluate the impact of interpretations at varying resolutions. In this work, we illustrate the workflow for four areas and geological models in the UK’s Southern North Sea: 1) Basin Scale (58,900 km2) - >48,800 TWh of hydrogen storage with >199,000 cavern locations. 2) Sub-Regional Scale (24,800 km2) - >9,600 TWh of hydrogen storage with >36,000 cavern locations. 3) Block Specific–Salt Wall (79.8 km2) - >580 TWh of hydrogen storage with >400 cavern locations. 4) Block Specific–Layered Evaporite (225 km2) - >263 TWh of hydrogen storage with >500 cavern locations. Our workflow enables reproducible and replicable assessments of site screening and storage capacity estimates. A workflow built around these ideals allows for fully transparent results. We compared our results against other similar studies in the literature and found that often highly cited papers have inappropriate methodologies and hence capacities.
Introduction
Long-duration energy storage (LDES) will be a critical feature of future energy systems (McNamara et al., 2022; Smdani et al., 2022). As renewable and low-carbon energy displace fossil fuels there will be a need to accommodate the increased variability of supply that comes with this transition (Dowling et al., 2020). LDES allows for the management of grid imbalances that arise from both the variable supply of renewable energy and the variability on the demand side while improving the overall flexibility and reliability of the energy system (Kueppers et al., 2021; Sepulveda et al., 2021). There are three principal mechanisms for geological LDES: mechanical (compressed air or solid weight), thermal, and chemical energy storage (e.g., hydrogen, ammonia, methane) (Bauer et al., 2013; Shan et al., 2022). Chemical storage is often considered the most versatile of these three options, as the energy storage medium can also be transported via pipelines or tanks and used with relative ease and with a lower energy cost (<0.1%) than when energy is transported for high-voltage energy cables (5%), over long distances, adding to the flexibility of the energy system as a whole (Calado and Castro, 2021).
Subsurface formations have proven to be suitable storage volumes over geological time scales, as evidenced by the occurrence of natural hydrocarbon accumulations (Lokhorst and Wildenborg, 2006). The subsurface has already been utilised since 1915 for the storage of natural gas, with the first site in operation in Ontario, Canada (Lord, 2009). More modern examples include the Rough gas storage field, located offshore the UK, which has been in operation since 1985 (with a 5-year hiatus from 2017 to 2022) with the capacity to store 54 BCF of natural gas (Centrica, 2023), or in Cheshire, UK, where Storengy operates a salt cavern cluster consisting of 28 caverns with the capacity to store 14 BCF of gas (≈4.1 TWh) (Eising et al., 2021). Hydrogen has also been stored within the subsurface; for example, the Spindletop salt cavern cluster in Texas, USA, which stored 5 BCF (≈1.45 TWh) of natural gas, was converted to store .274 TWh of hydrogen (Bérest et al., 2021). Compared with other methods of LDES, such as Li-Po batteries and pumped hydro, subsurface geological storage, also known as Underground Energy Storage (UES), provides several advantages, including greater capacities, a small surface footprint, low operating costs, operational timespans of over 30 years, and increased safety (Crotogino et al., 2017). There are two differing subsurface storage methods: porous media (e.g., saline aquifers and abandoned hydrocarbon fields) or salt caverns (Evans, 2007; Bauer et al., 2013). Salt caverns for hydrogen storage are the option investigated in this study, as, while research has been undertaken on hydrogen storage in porous media such as Heinemann et al. (2018), Heinemann et al. (2021), Hassanpouryouzband et al. (2022), storage of hydrogen in porous media is in its infancy with only demonstrations in operation, with the first injection in the early 2020s, whereas there are several salt cavern clusters storing hydrogen currently in operation, the first of which started operation in the 1960s (Evans, 2007; Underground Sun Storage, 2023).
Salt caverns are solution-mined voids within evaporitic (salt) layers (Warren, 2006; Tarkowski and Czapowski, 2018). They range volumetrically from 70,000 m3[e.g., Teesside, UK (HyUnder, 2013)] to 17,000,000 m3 [Texas (Leith, 2000)]. Salt caverns are an established technology that has been in use since the 1960s for storing gas (Allen, 1971; Allen et al., 1982). Hydrogen has been stored within salt caverns since the early 1970s for use in the chemical industry, with the first site located in Teesside, UK (Landinger et al., 2007; Caglayan et al., 2020; François, 2021) and Texas. Although recently published work on salt cavern volumetrics has mostly focused on onshore areas, there are few that focus on offshore areas. These works frequently investigate country-wide scale analyses for capacity estimates and cavern placement (e.g., Caglayan et al., 2020; Williams et al., 2022; Allsop et al., 2023), with modelled capacity estimates across entire basins greatly exceeding the estimated requirements for LDES for the UK’s energy transition requirements (Cárdenas et al., 2021; Ofgem, 2021). Current estimates rely on geological models with limited resolution and are not able to capture the geological complexity of both the salt layers and the overburden. Simplified, or basic geological models may not reliably estimate cavern placement options and their storage capacity. While there have been assessments of the geological constraints on offshore salt cavern development in the UK, notably by Allsop et al. (2023) and Caglayan et al. (2020), these have not utilised a systematic approach. Offshore salt caverns are not outside the realm of technical feasibility (Costa et al., 2017). One of the possible benefits of offshore storage is the co-location of storage next to offshore wind farms, or pre-existing pipelines (which will require modification or replacement to be hydrogen compliant), thus developing a hub for both energy production and storage. Salt caverns are typically developed in clusters (Gillhaus, 2007) and the work here could be considered as the basis for pre-feasibility studies of cavern placement options.
Here, we demonstrated the robustness and flexibility of our methodology for the UK offshore. The UK is currently undergoing a shift in the supply of energy to meet its 2050 net-zero obligations, with installed wind power capacity reaching 27.9 GW in 2023 (Staffell et al., 2023). For 100% renewable penetration in the UK by 2035, Cárdenas et al. (2021) found that with the optimal mix of renewable technologies and allowing for over-generation, the UK would require ∼43 TWh of LDES, far less than the suggested 115 TWh needed if no over generation was allowed. The UK’s Electricity System Operator (2023) stated that a full energy system transformation would require the UK to have 56 TWh of hydrogen storage by 2050. Without the utilisation of LDES in the energy mix it will be difficult for the UK to achieve its legislated net-zero carbon goals (King et al., 2021). Geological storage is currently the most viable option for LDES in the UK as: 1) there are a number of possible location options distributed across the UK, and the location of storage is an important consideration in the overall system (Sunny et al., 2020); 2) pre-existing oil and gas infrastructure could be repurposed to reduce the capital expenditure associated with LDES scale up (Oil and Gas Authority, 2021); 3) Geological storage is currently estimated to be one of the lowest cost LDES options available (Hunter et al., 2021; The Royal Society, 2023).
We have focused on the Southern North Sea area of the UKCS due to data availability, geological suitability, and possible future demand for hydrogen storage within the area. Four areas of interest (AoIs) were defined within our study (Figure 1) to consider the potential locations and capacity of salt caverns for hydrogen storage within the Zechstein Supergroup. The Zechstein Supergroup is a Late Permian layered evaporite sequence deposited during the Lopingian (Peryt et al., 2010). It is laterally extensive and exceeds 750 m in thickness over large areas, of which only a portion is pure halite that can be utilised for cavern placement (≈40% in layered sequences and ≈80% in structured areas). It is located in both the North Permian and South Permian Basins of Europe, where it extends from the onshore of the east coast of the UK, across to western Poland. (Glennie, 1998; Fyfe and Underhill, 2023). The Zechstein Supergroup is found as both layered and structured salt in both basins. The current understanding of the Zechstein Supergroup comes from both the hydrocarbon exploration industry, where it is important for trapping mechanisms and sealing of reservoir intervals, and the onshore mining industry (notably in Europe), where further understanding of the internal composition and structuring originates (Glennie, 1998; Raith et al., 2016; Strozyk, 2017; Doornenbal et al., 2019; Grant et al., 2019; Pichat, 2022). The deposition of the Zechstein supergroup as a layered evaporite sequence is commonly divided into five cycles; however, the nomenclature used frequently varies depending on regional location and depositional setting (Johnson and Stoker, 1993; Fyfe and Underhill, 2023). The internal heterogeneity of the Zechstein varies in complexity across the Southern North Sea due to the mobility of the Zechstein from halokinesis (Barnett et al., 2023).
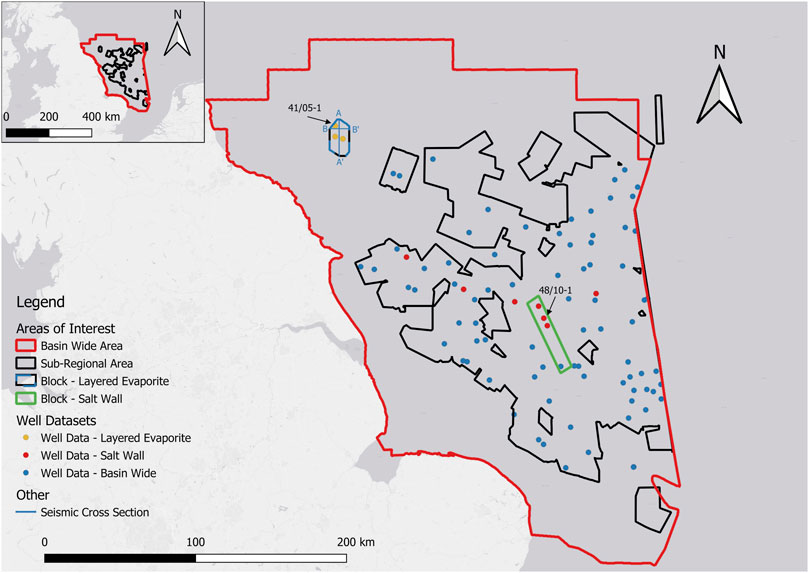
Figure 1. Location map of areas of interest (AoIs), off the East coast of the UK. AoI locations are labelled and shown on the map. Well data used in the “Block – Layered Evaporite” area are marked on, along with seismic cross sections (Figure 3). Map 2, (top left) details the extent of the study areas in relation to the whole of the UK and Northern Europe. Well data were used to derive the insolubility content for each area present (it should be noted that all salt wall wells are located within diapiric structures).
In this paper “salt” is used as a general term to refer to a vertical extent of evaporites, which typically comprise mostly halite, but with non-halite heterogeneities present. A salt unit refers to a stratigraphically recognised vertical section of salt that is part of a larger evaporite group.
Methodology
Workflow
The workflow developed uses a geological model as input, determines an idealised cavern layout and calculates the potential working hydrogen storage capacity (Supplementary Appendix S1). Due to the inherent uncertainty associated with geological models, the method can accommodate both single values and distributions. The workflow is agnostic to the resolution of the input geological model, recognising that the availability of data varies from area to area, allowing investigations from site to basin scale. The method can incorporate distribution-based inputs in which case the workflow is run as a Monte Carlo simulation, capturing the inherent uncertainty of the geological model. The workflow is a reproducible and reliable method to determine the placement of salt caverns and calculate the hydrogen storage capacity. It can be set to optimise either the number of caverns or the capacity, allowing for an idealised utilisation of the area of interest.
The workflow initially removes areas of the geological model that have been determined as being unsuitable based on the set parameters (Supplementary Appendix S1). The suitability of these areas for cavern placement is treated as a binary condition, either more or less suitable. It is possible to incorporate both geological and surface constraints, such as faults and heterogeneous salt areas mapped by seismic surveys, or roads and populated areas in onshore areas. Buffers can be applied to these features, which then determine a set distance for cavern placement.
The depth of geological formations can be constrained using seismic data and well data, where depth-calibrated measurements from wells are used to interpret formation reflections within seismic data. As a result, depths in geological models have an inherent level of uncertainty. We have accounted for this by using a uniform distribution calculated from the residual depth values calculated during the depth conversion process. The largest residual value from the depth conversion process was calculated as a percentage and both the positive and negative limits of the uniform distribution were set. As depth uncertainty can be either positive or negative, setting the maximum residual to limit the uniform distribution (e.g., −10% and +10%) allows the workflow to account for depth uncertainty.
The workflow assumes that each grid cell within the geological model that has not been removed is a potential location for cavern placement. The height-to-diameter ratio at each potential location is determined by using the salt thickness at that location (Supplementary Appendixs S1, 2). A cavern geometry is determined from the salt thickness and height-to-diameter ratio (Supplementary Appendixs S1, S2; Supplementary Appendix Equations SA–E (Caglayan et al., 2020)], with a maximum cavern height limit of 750 m; however, this can be adjusted as required. If fixed cavern geometry is used, then the pre-set cavern height and diameter are used instead.
Caverns are typically developed in salt below a depth of 500 m, as this enables larger caverns with higher working gas capacities (Warren, 2006; Caglayan et al., 2020; Tan et al., 2021). However, it is worth noting that onshore caverns within the UK have been developed at depths as shallow as 300 m where there can be advantages due to reduced drilling, the proximity to other infrastructure, and the required volumes may be adequate (Parkes et al., 2018). In this study we have modelled scenarios where caverns are at a minimum depth of 500 m. To accomplish this, if a possible cavern location is in a location where the top salt is < 500 m, it is checked to see whether the salt interval extends deeper than 500 m and has sufficient thickness beyond 500 m depth for the cavern geometrical requirements. This optimisation allows for higher operating pressures, and therefore higher hydrogen capacities in areas of shallow but thick salt [Supplementary Appendix S1; Equation 1 (Fanchi and Christiansen, 2016)]. The workflow is modifiable so that if a shallower cavern placement is required it can be adjusted as needed.
E = Energy Hydrogen (TWh)
P =
R =
V =
T =
The minimum distance between cavern midpoints (buffer distance, Figure 2) is then determined to establish a feasible combination of adjacent cavern locations (Supplementary Appendix S1; Supplementary Appendix Equation SG) and is a simplified approach to account for the geomechanical requirements for stability between adjacent caverns (Caglayan et al., 2020; Ma et al., 2022). If the grid cell spacing is greater than the buffer distance between caverns then there will be overlap between buffers. To determine a layout where there is no buffer overlap, the workflow iterates in the x coordinate through the array of potential cavern locations starting at 0,0 (top left), plots a cavern, checks to see if the buffer overlaps with another cavern’s buffer, and if it does not, keeps it, while if it does, it is deemed unsuitable and removed. Further details of this method can be found in the Supplementary Appendix under “Further information - cavern best fit algorithm.” This methodology optimally packs the caverns within the areas with the potential for cavern placement.
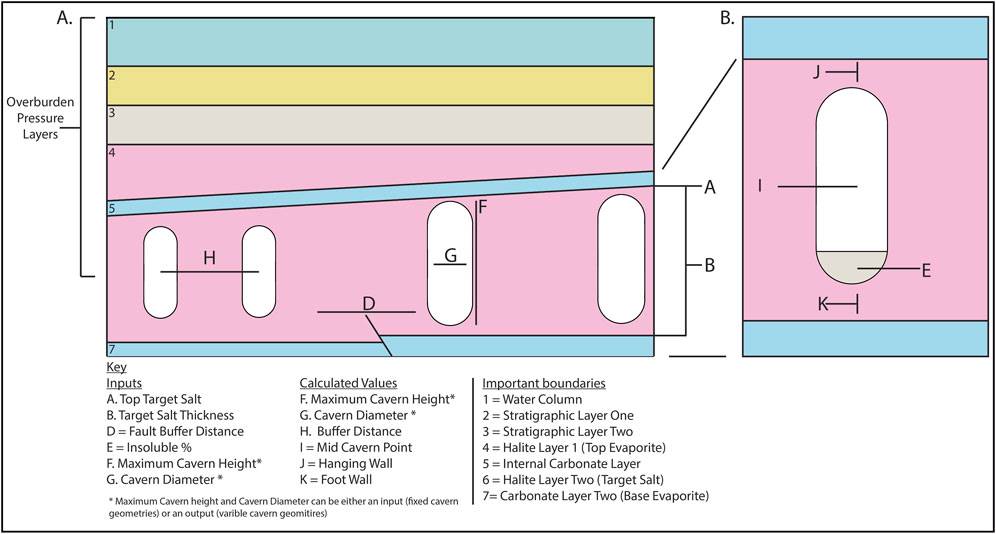
Figure 2. (A) Cartoon schematic geological cross-section of emplaced salt caverns (Not to scale). Important parameters (both inputs and calculations) for the characterisation of a salt cavern site have been labelled A–K, and overburden characterisation 1–7. (B) The diagram shows an individual cavern and the parameters considered for individual cavern placement.
The volume is then calculated for each cavern (Supplementary Appendix S1; Equation 2). For caverns with a height-to-diameter ratio of <1, an ellipsoid shape was assumed for the volume (Supplementary Appendix S1; Supplementary Appendix Equatiion SH), as capsule geometries become ellipsoids with a height-to-diameter ratio of <1. The volume of the cavern will depend on its planned geometrical shape. Our workflow uses capsule geometries for the 3D cavern shape (Figure 2), as these are the most stable and have the lowest stress risk (Ozarslan, 2012).
V =
H =
r =
This leaves all potential cavern locations within the area with suitable spacing and geometry for the salt layer in the geological model. The lithostatic pressure for the mid-cavern depth is calculated as it determines the cavern operating pressure. A simple 1D layer cake approach can be used to calculate the lithostatic pressure Equation 3 (Zoback, 2010) or a simple gradient approach depending on the data available (Overburden Pressure). For layer cake models, the same depth uncertainty is applied to that of the salt depth and thickness surfaces. Uncertainty in the density of the overburden layers may also be included. Internal cavern temperatures are calculated using a geothermal gradient and mid-cavern depth (Equation 4; Temperature). The geothermal gradient used can be either a fixed value or be derived from a distribution (Supplementary Appendix S3).
The cavern volume is then adjusted to account for the insoluble content that is present in the salt (Supplementary Appendix S1; Supplementary Equation SJ; Temperature). A simple % can be used, a distribution derived from well data, or a map (Supplementary Appendix S4). Geomechanical instability with raised levels of insoluble content is not accounted for in this workflow. A shape correction factor is incorporated to account for the change in the planned cavern geometry due to non-halite content (Williams et al., 2022). As insoluble content will modify the shape of the emplaced cavern, the value of the shape correction factor was correlated to the insoluble content % (Warren, 2016). A linear relationship between insoluble content and a shape correction factor was assumed after a shape correction factor was calculated (Supplementary Appendix S5).
The individual cavern hydrogen capacity is then calculated using the ideal gas law [Equation 1 (Fanchi and Christiansen, 2016)]. The working capacity is calculated based on 60% of the lithostatic pressure at mid cavern depth, with a cushion gas of 20% to maintain cavern integrity and a maximum pressure in the caverns of 80% to avoid exceeding the fracture gradient (Ozarslan, 2012; Caglayan et al., 2020; Muhammed et al., 2022). Once the individual capacity of each cavern has been calculated, the energy capacity for the whole area or a cavern cluster can be determined (Supplementary Equation SK, L). The energy capacity calculations are modifiable to allow for different energy vectors, such as natural gas, ammonia, or other gases or fluids.
From the Monte Carlo simulation, p10, p50, and p90 values can be calculated. The outputs from this workflow include not only numerical capacity and cavern number but also geospatial data.
Model Parameters
The geological model requires parameterisation of the following, insoluble content, geothermal gradient, and pressure. These can be determined from both well and seismic data.
Overburden Pressure
Two separate approaches can be taken depending on the data available. 1) For areas where data for the above layers of the overburden are available along with density data, a layer cake approach was used [Equation 3 (Zoback, 2010)]. As the geological surfaces used for thickness calculations are affected by the uncertainty in the depth conversion, these values were modified to the same uncertainty distribution as applied to the geological surfaces. Bulk density well logs were used to calculate the average densities for each of the geological layers in Supplementary Appendix S1–Supplementary Appendix Equation S9. These values are also subject to a certain level of uncertainty, so to account for this it was decided to apply a uniform distribution of +-10% to the densities in each model run. This was not applied to the water column layer, instead, a constant value of 1024 kg/m3 was applied.
Ln =
2) For areas where the data were not available to construct a layer cake model, a simple 2-layer depth/gradient approach was used which accounted for both the water column and rock overburden separately. The gradient of the rock overburden was calculated from the average overburden density, a value of 1024 kg/m3 assumed for the water column and the depth taken from the cavern mid-point (Supplementary Appendix Equation S1).
Temperature
The geothermal gradient was calculated using the principle for determining geothermal gradients from Allen and Allen (2013). Bottom well temperatures were examined from wells within the AOI to calculate the geothermal gradients. From these calculated gradients, minimum and maximum gradients were extracted. The minimum and maximum values set the bounds of a uniform distribution for the geothermal gradients to be used in the calculation of the mid-cavern temperature (Supplementary Appendix S1, S3). The geothermal gradient was then used in Equation 4 to calculate the cavern temperature.
Insoluble Content
The insoluble content of the AOI was calculated from available well logs within the area. Insoluble content was identified as all siliciclastic and carbonate lithologies present within the well; the evaporitic minerals anhydrite and polyhalite were also included in the insoluble content criteria, due to their high level of insolubility compared with halite (Warren, 2016). From the calculated insoluble content values, a distribution was created to be used within the workflow.
Equation 5 is modified from an equation for net to gross from Alyafei (2021).
Sensitivity Analysis
A sensitivity analysis was undertaken for two separate AOIs and geological models, the layered evaporite block and the salt wall block (Layered Evaporite - Variable Cavern and Salt Wall). A Sobol sensitivity analysis used 1000 iterations and was implemented with the use of the SALib python module (Sobol, 2001; Herman and Usher, 2017; Iwanaga et al., 2022). For the sensitivity analysis, four parameters were included: depth uncertainty, geothermal gradient, insolubility, and overburden gradient.
Geological Model Building
Geological Model Methodology
Well Data Interpretation
Petrophysical logs were interpreted to distinguish different lithologies and different stratigraphic intervals. A combination of gamma-ray, sonic, and density logs was used alongside the geological descriptions of the well site from cuttings. For the Zechstein Supergroup stratigraphy, however, lithologies were applied at the highest resolution allowed by the petrophysical logging tools. This resolution varies depending on the type of logging tool used but it typically ranges from 1 to 5 m (Bourke et al., 1989). Following this, well tops were applied to the intra-Zechstein stratigraphy, using the same QC as used for the non-Zechstein stratigraphy. This well interpretation allowed for the interpretation of the key geological horizons within the seismic data.
Seismic Well Tie
Synthetic-seismic well ties were generated to correlate the interpreted stratigraphic boundaries from the well data, which were in the depth domain (m) to the seismic data which were in the time domain (ms). Synthetic traces were generated using a 35 hz ricker wavelet and extracted wavelets. These were compared with the original seismic data and the best match was selected to be used. The wells were bulk-shifted vertically to ensure the best possible time-depth match between the well and seismic data, aiming to match the top Zechstein seismic reflection by the bulk shifting process.
Seismic Data Interpretation
Reflections identified as key stratigraphic boundaries were interpreted on the seismic data. Reflections of stratigraphic boundaries were initially mapped at intervals of 25 m on both crosslines and inlines. 3D auto-tracking was used to complete the horizon interpretation. If areas were not sufficiently mapped by the auto-tracking process, they were manually remapped in smaller increments and then re-auto-tracked. This process was repeated until suitable interpretations of each key reflection had been achieved. From these reflection interpretation horizons, surfaces were generated that had a grid spacing of 50 × 50 m and used a convergent gridding algorithm. This process produced seamless surfaces.
Geological faults were mapped from the seismic data. To accomplish this, the seismic data were viewed perpendicular to the strike of the fault. Intersection intervals of 25 m were used, with the view of the seismic data being re-oriented as the fault orientation changed. Faults were mapped until they were no longer interpretable within the seismic data.
Seismic Depth Conversion
Depth conversion is required where seismic data are in the time domain, as all calculations used to determine cavern placement and geometry require depth as a constraint. For depth conversion, we follow a standard approach of using geophysical logs to determine the velocity structure in the subsurface (Al-Chalabi, 2014). This is subsequently used to determine interval velocities for the layers within the geological model. Time-depth relationship data were extracted from wells within the area, the generated time surfaces were then used in conjunction with the velocity values extracted and identified velocity interval to create depth surfaces. The final output models aimed for residuals of <10%. For a complete description of the depth conversion method please see the data repository.
Geological Models
In the sections below we describe the different geological models and their parametrisations used as case studies for the workflow described. Three discrete sets of depth surfaces were used for the four areas of investigation. These depth surface datasets have different resolutions and different associated depth uncertainties. The basin-wide, sub-regional and salt wall depth surfaces were derived from existing available interpretations, while the layered evaporite model had surfaces interpreted for this study using the methodology described in Well Data Interpretation–Seismic Depth Conversion. Data from different sources were used to investigate the response of the proposed workflow at different data scales, resolutions, and uncertainties.
Basin-Wide Salt Depth Model
The basin-wide depth model covers an area of 58,904 km2 (Figure 1). The surfaces used in the model have a grid cell size of 250 m × 250 m (the lowest resolution of the depth models used) and bound the top and base Zechstein Supergroup. The surfaces are from the “NSTA and Lloyd’s Register SNS Regional Geological Maps (Open Source)” dataset and are available from the NSTA public open data repository1. No information was supplied regarding depth uncertainty. We assumed a 10% depth uncertainty to account for this.
Sub-Regional Salt Depth Model
The depth surfaces for the sub-regional salt depth model are from Barnett et al. (2023) and cover 25,000 km2 (Figure 1). The surfaces are from the interpretation of a regionally extensive 3D merge seismic volume of the Southern North Sea (OA__2019seis0001a), with the top and base surfaces using bounding top and base Zechstein, and the surfaces having already been converted from the time to depth domain. The grid cell size is 50 m × 50 m. The depth surfaces have a 5% uncertainty associated with them (Barnett et al., 2023).
Block Specific
Blocks, in the context of the offshore energy industry, define set areas where licences have been granted for specific activities, such as oil and gas exploration, or more recently, carbon capture and storage. Gas storage licences are also awarded as blocks by the UK’s North Sea Transition Authority, with Centrica being awarded a licence for the Rough Gas storage site in 2022 (North Sea Transition Authority, 2022). Exploration blocks in the Southern North Sea are on average 115 km2, with the largest being 250 km2. We aimed to mimic these spatial constraints when applying our workflow, as it is likely that licences and areas for gas storage in salt caverns will be granted in a similar manner by the North Sea Transition Authority.
Salt Wall Salt Depth Model
The depth surfaces from the salt wall cover an area of 420 km2 (Figure 1). It is located on a structure often referred to as the Audrey salt wall (Elam, 2007; Allsop et al., 2023), which trends NNW – SSW in the UK sector of the South Permian Basin. The depth surfaces were extracted from the Sub-regional depth model, and thus the grid cell size of 50 m × 50 m and depth uncertainty of 5% remain the same.
Layered Evaporite Salt Depth Model
The layered evaporite salt depth model covers an area of 225 km2 (Figure 1). It is located on the northern edges of the South Permian Basin, just south of the Mid-North Sea High (Figure 1). The MA933F0002 seismic survey was used to interpret the top and base target salt, and other major stratigraphic reflections for the area (Supplementary Appendix Table SA). The reflection chosen as the top target salt was the top of the Stassfurt Halite and the base target salt was the Basel Polyhalite of the Stassfurt Halite because this was the thickest and most homogeneous section of halite in this section in the interpreted well data (Figures 3, 4). Seismic reflections in layered evaporite sequences can be difficult to interpret. Fortunately, the targeted reflections within the seismic data set were mostly continuous and could be interpreted. However, in areas where seismically resolvable high internal structural heterogeneity and deformation were present, the targeted reflection could not be interpreted with a high degree of confidence. As these areas contained seismic heterogeneities that indicated that the area had no potential for cavern emplacement, a best effort was made to map the target reflections and the area of internal structural heterogeneities was mapped in a time slice view to be used as an input within the geological model as an area not suitable for cavern emplacement. Two-way time surfaces were created as described in Seismic Data Interpretation from the interpreted seismic reflections. As the surfaces were in two-way time, they had to be depth converted. The depth conversion model used 5 layers (Supplementary Appendix Table SA, excluding the base Zechstein) and time-depth relationship data were taken from two wells in the area (See Data Repository). The final depth surfaces had a grid cell size of 50 m × 50 m, and a residual uncertainty of 7%. Within the Stassfurt Halite there were heterogeneities observed that were interpreted to be non-halite (insoluble) lithologies. These heterogeneities cannot always be interpreted on seismic data due to the abrupt termination and discontinuity of the seismic reflections within the area (Barnett et al., 2023). The area where these heterogeneities were observed was instead mapped using seismic time slice views within the Stassfurt Halite (Supplementary Appendix S6). These mapped heterogeneities were included in the geological model as areas incompatible with salt cavern placement.
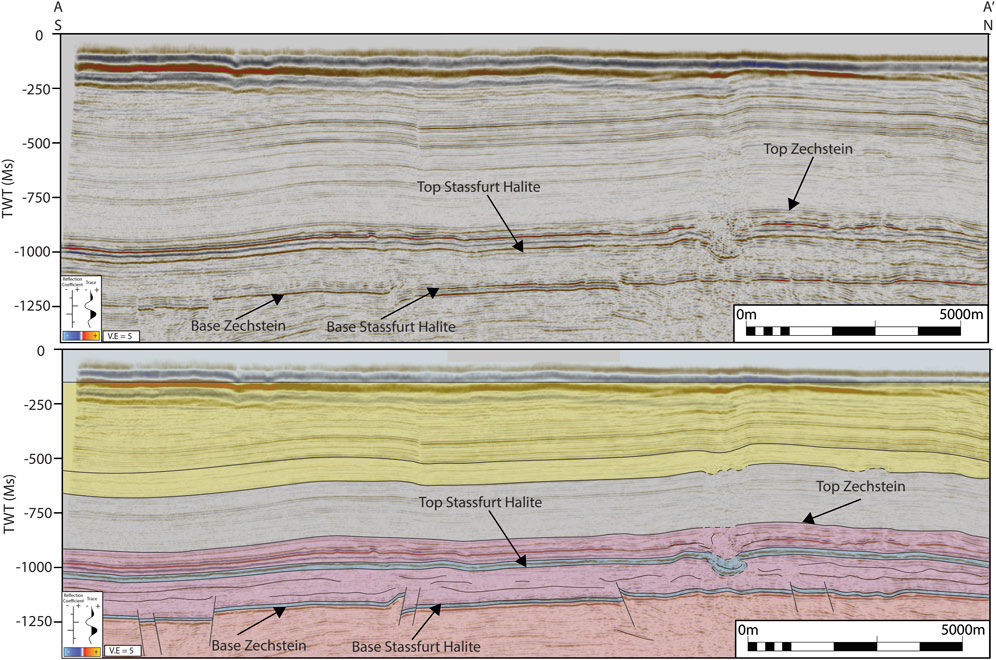
Figure 3. Example of a seismic cross-section from the “Block – Layered Evaporite” AoI (Seismic Survey MA933F0002), running North to South, A–A’ (Figure 1), in TWT, key reflections have been marked on.
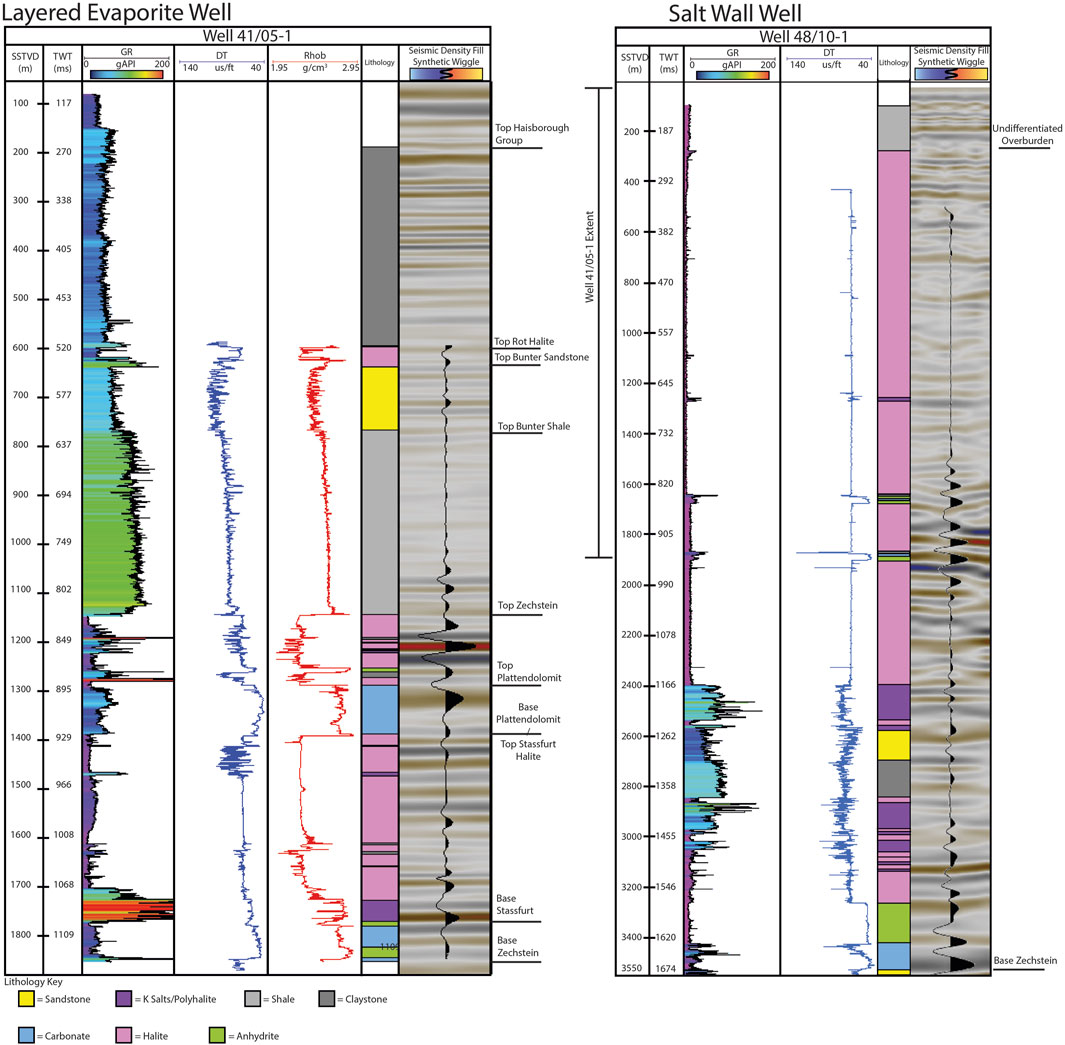
Figure 4. Petrophysical logs from wells 41/05-1 and 48/10-1 (Figure 1), GR (gamma ray), DT (sonic), Rhob (density), interpreted lithology log is present. Calculated synthetic seismic wiggle overlying seismic trace from seismic survey MA933F002 and interpreted key stratigraphic boundaries.
Geological Model’s Parametrisation
Seven separate geological models were developed using the five depth models in Geological Models (Supplementary Appendix Table SB). The models were designed to investigate the effect of different scales, cavern design, data quality and salt type on cavern placement. Parameters for the workflow, such as minimum salt thickness and maximum depth were taken from the literature and can be found in Supplementary Appendix Table SC. Each AOI had a distribution of insoluble content calculated from wells within the area to account for non-halite lithologies present within the cavern column (Figure 1, Same distribution applied to basin-wide and sub-regional). Each geological model investigated (Supplementary Appendix Table SB) was run as a Monte Carlo simulation for a total of 2500 iterations.
Results
Basin Wide
Basin Wide – Fixed Caverns
The p50 cumulative storage capacity from the basin-wide geological model is 48,875 TWh (Figures 5A, B). The p90 and p10 capacities are 39,570 and 64,438 TWh, respectively. This is based on a total cavern number of 195,563 for the p50, 161,876 for the p90 and 252,614 for the p10. The average cavern capacity for the Monte Carlo iteration closest to the p50 value (iteration 149) is 245 TWh. Iteration 1808 of Monte Carlo is the geospatial representative of the p50 capacity and can be seen in Figure 5A. Individual cavern capacities are typically lower towards the edges of the basin and placement in the basin depocenter is typically restricted to salt structures (Figure 5).
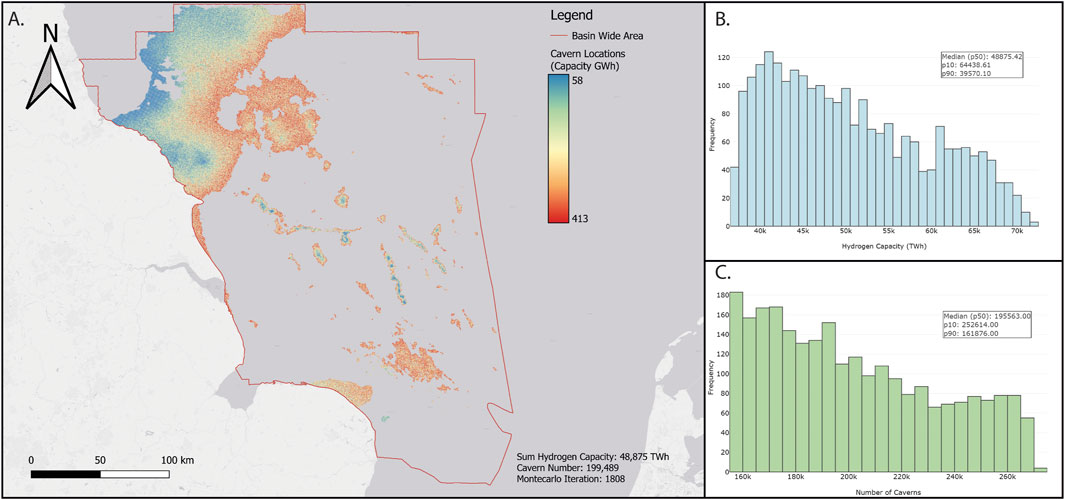
Figure 5. (A) “Basin Wide” AoI cavern placement map, fixed cavern geometries. The geospatial placement represents the output model from the workflow with the total hydrogen capacity closest to the calculated p50 (Iteration 1808/2500). A total of 199,489 caverns are placed, with a sum of 48,875 TWh of hydrogen storage capacity. (B) Histogram of total hydrogen capacities for each iteration of the Monte Carlo simulation (2500 iterations). (C) Histogram of the total number of caverns for each iteration of the Monte Carlo simulation (2500 iterations).
Sub-Regional
Sub-Regional – Fixed Caverns
The p50 capacity of the sub-regional basin-scale geological model is 9,685 TWh, and the p90 and p10 are 8,045 and 12,579 TWh, respectively (Figures 6A, B). This is based on a total cavern number of 35,873 for the p50, 30,086 for the p90 and 46,230 for the p10 (Figure 6C). Iteration 2011 of the Monte Carlo simulation is the geospatial representative of the p50 result and can be seen in Figure 6A. The locations identified for the development of caverns predominantly show that cavern placement in the mid basin follows the orientation of the major salt structures. In total, 27.4% of caverns in the p50 model are plotted in salt walls and diapirs, despite walls and diapirs only accounting for 5.6% of the total area of the sub-regional basin area (1,400 km2). The remaining 72.6% of caverns are plotted at the basin edges to the northwest towards the Mid-North sea high, where the cavern placement occurs within areas of layered evaporite and hence cavern placement is more ordered (Figure 6).
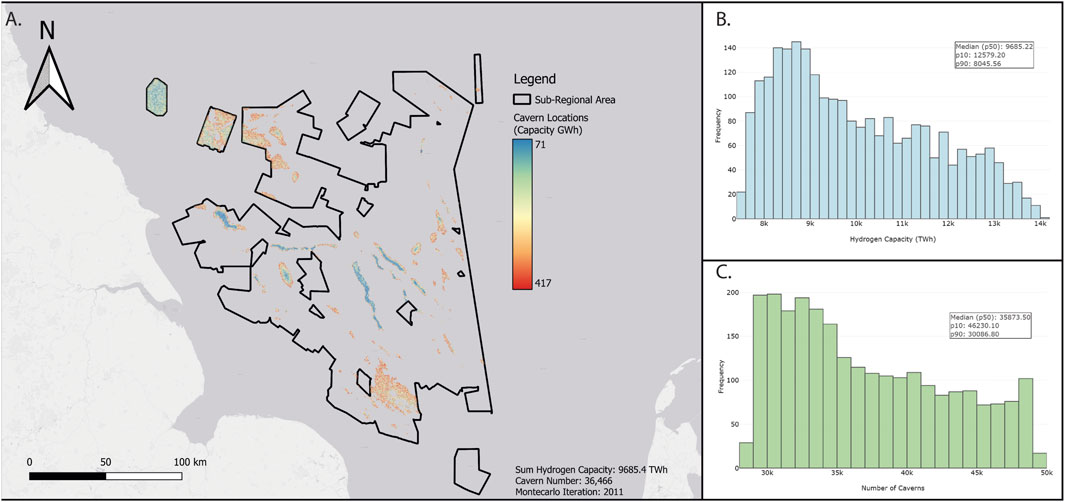
Figure 6. (A) “Sub-regional” AoI cavern placement map, fixed cavern geometries. The geospatial placement represents the output model from the workflow with the total hydrogen capacity closest to the calculated p50 (Iteration 2011/2500). A total of 36,466 caverns are placed, with a sum of 9,685 TWh of hydrogen storage capacity. (B) Histogram of total hydrogen capacities for each iteration of the Monte Carlo simulation (2500 iterations). (C) Histogram of the total number of caverns for each iteration of the Monte Carlo simulation (2500 iterations).
Block Specific
Salt Wall
Salt Wall - Variable Cavern
The p50 capacity of the salt wall – with variable cavern sizes, is 580 TWh, with the p90 and p10 capacities being 562 and 580 respectively (Figures 7A, B). We identified 409 potential cavern locations in the salt wall (Figure 7A). Despite the stochastic approach applied to the salt surfaces to account for depth uncertainty, as the interpreted salt thickness is typically greater than 2500 m the 5% depth uncertainty does not affect how many caverns can be placed. As such all caverns were set to the maximum possible height of 750 m (Supplementary Appendix Tables SB, C) and hence had the same height-to-diameter ratio applied to them. This resulted in all caverns having the same volume of 5,628,686 m3 before adjustment for both insoluble content and shape correction factor.
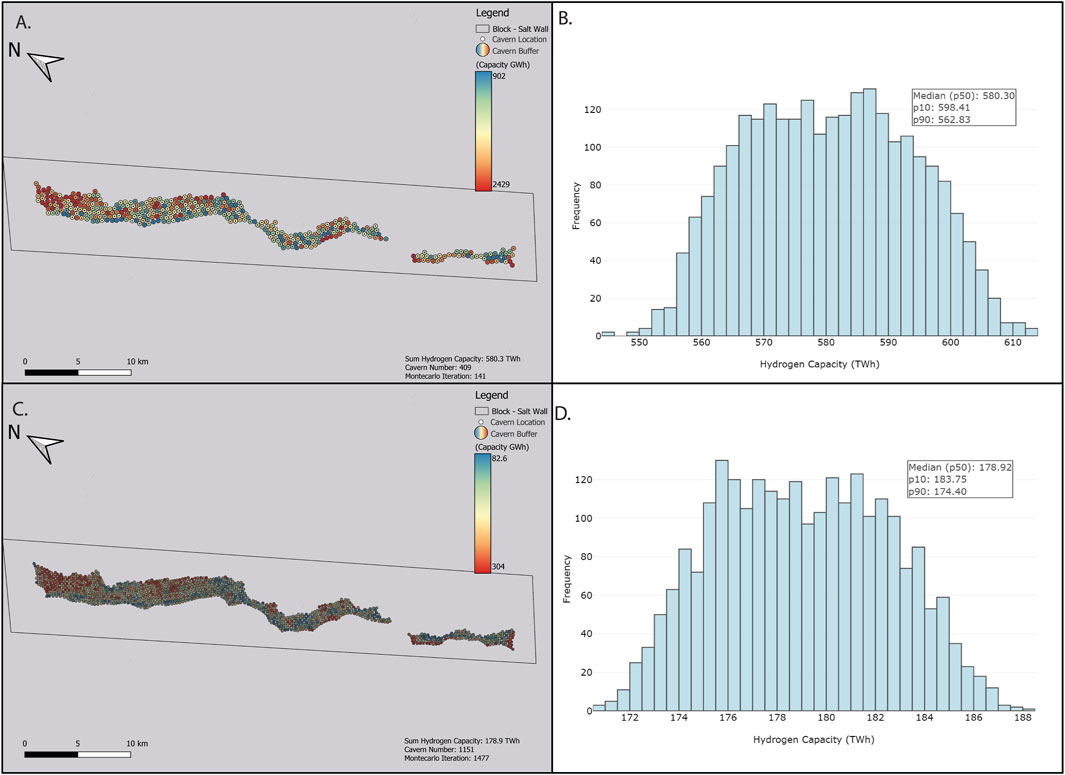
Figure 7. (A) “Block Specific – Salt Wall” AoI cavern placement map, variable cavern geometries. The geospatial placement represents the output model from the workflow with the total hydrogen capacity closest to the calculated p50 (Iteration 141/2500). A total of 409 caverns are placed, with a sum of 580.3 TWh of hydrogen storage capacity. (B) Histogram of total hydrogen capacities for each iteration of the Monte Carlo simulation (2500 iterations). (C) Cavern placement map for the “Block Specific – Salt Wall” AoI, fixed cavern geometries. The geospatial placement represents the output model from the workflow with the total hydrogen capacity closest to the calculated p50 (Iteration 1477/2500). A total of 1151 caverns are placed, with a sum of 178.9 TWh of hydrogen storage capacity. (D) Histogram of total hydrogen capacities for each iteration of the Monte Carlo simulation (2500 iterations).
Salt Wall - Fixed Cavern
The p50 capacity of the salt wall geological model with fixed geometry caverns (Supplementary Appendix Table SB) was 178 TWh, the p90 and p10 results are 174 and 183 TWh (Figures 7C, D). The total number of potential cavern locations in the area ranges between 1151 and 1154, depending on the depth uncertainty applied (Figures 7C, D). Small edge case variations between the Monte Carlo iterations caused by the associated depth uncertainty %, cause small areas to become theoretically viable or unviable, causing the small change in cavern number, similar to that of the variable salt wall cavern number.
Layered Evaporite
Layered Evaporite - Variable Cavern
The p50 capacity of the layered evaporite–variable cavern geological model is 263.1 TWh, and p90 and p10 are 242.2 and 283.0 TWh, respectively. For p50 the number of potential cavern locations is 440 (Figure 8; Table 1) with 358 and 495 for the p90 and p10 respectively (Figure 8; Table 1). Table 1 shows the closest model iteration output to the p10, p50, and p90 capacity values (Figure 8). The iteration closest to p50 has the largest number of caverns present but has the smallest working average cavern working capacity of .524 TWh compared with .596 TWh for p90 and 198 TWh for p10. The iteration closest to the p10 and p90 capacity values has a similar number of caverns placed (408 and 406), but the P10’s larger average working capacity gives the model a larger total working capacity.
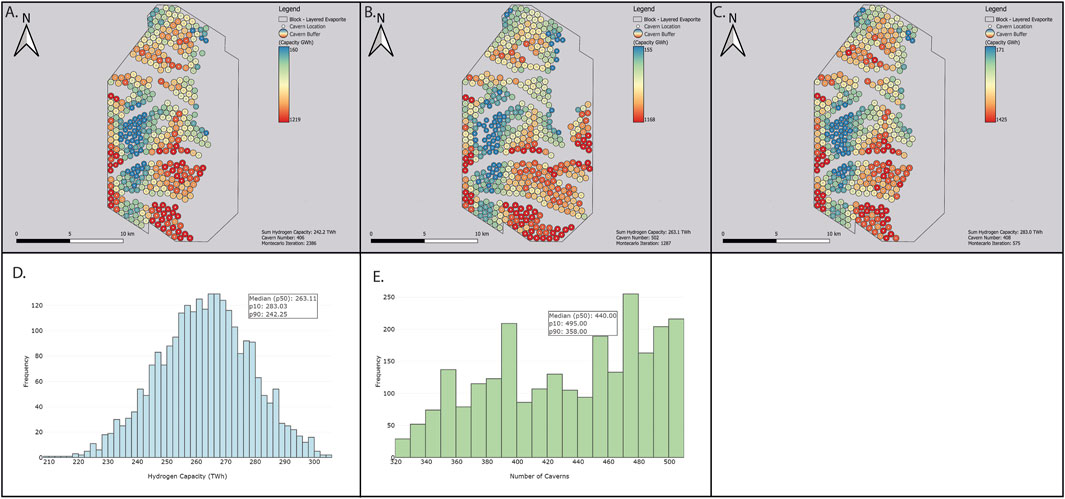
Figure 8. “Block Specific–Layered Evaporite” AoI cavern placement map, variable cavern geometries. Geospatial placement represents the output model from the workflow with the total hydrogen capacity closest to the calculated p90 [(A), Iteration: 2386], p50 [(B), Iteration: 1287], and p10 [(C), Iteration: 575]. (D) Histogram of total hydrogen capacities for each iteration of the Monte Carlo simulation (2500 iterations). (E) Histogram of the total number of caverns for each iteration of the Monte Carlo simulation (2500 iterations).
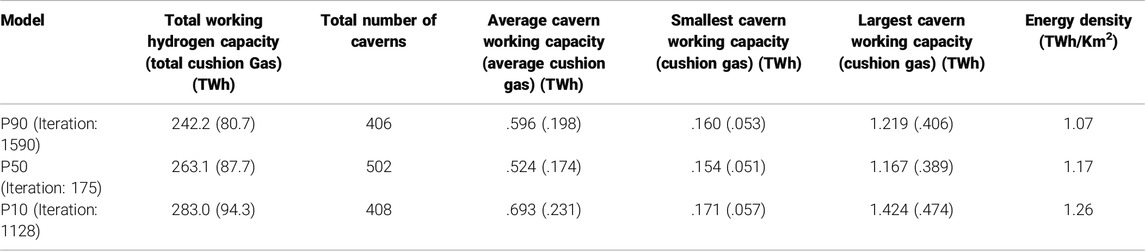
Table 1. Monte Carlo simulation results, iterations closest to p values from Layered evaporite – Variable cavern geometries.
Layered Evaporite - Fixed Cavern
The p50 capacity of the layered evaporite–fixed cavern geological model is 161.9 TWh (Figures 9A, C), 101.2 TWh less than that of the variable cavern model for the same AoI (Figure 9). The p90 and p10 capacity values are 106.6 and 178.8 TWh respectively. The p50 for cavern placement is 780, the p90 and p10 for cavern number are 519 and 820 potential locations. The iteration from the Monte Carlo simulation with the closest hydrogen value to the p50 capacity has a total of 806 potential cavern locations, 304 more caverns than the equivalent variable cavern p50 iteration. However, the fixed caverns have a much lower average capacity, with a value of .208 TWh, compared with .524 TWh for the variable caverns.
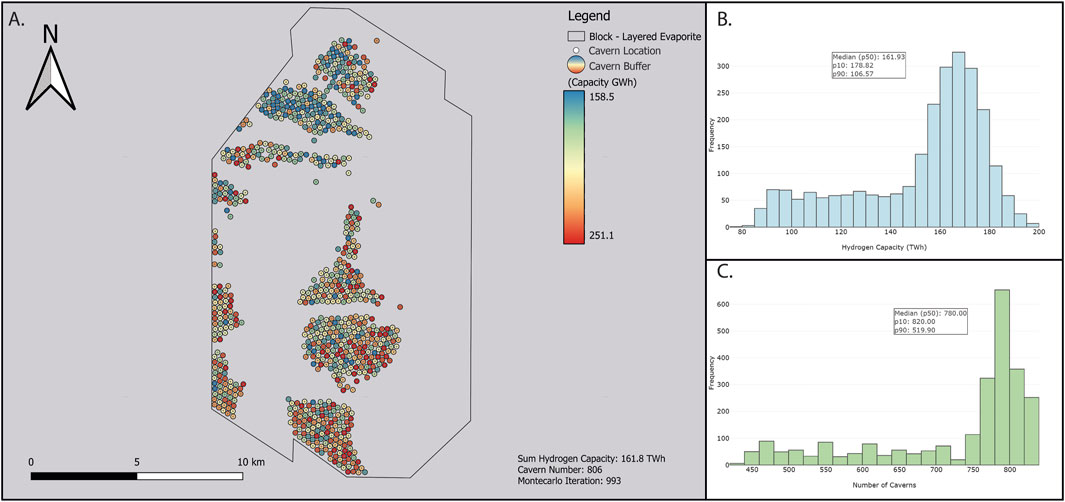
Figure 9. (A) “Block Specific – Layered Evaporite” AoI cavern placement map with fixed geometries. The geospatial placement represents the output model from the workflow with the closest total hydrogen capacity to the calculated p50 (Iteration 993/2500). A total of 806 caverns are placed, with a sum of 161.8 TWh of hydrogen storage capacity. (B) Histogram of total hydrogen capacities for each iteration of the Monte Carlo simulation (2500 iterations). (C) Histogram of the total number of caverns for each iteration of the Monte Carlo simulation (2500 iterations).
Layered Evaporite - Basin Wide Depth Model – Variable Cavern
The p50 capacity of the layered evaporite – basin wide depth model - variable caverns is 683 TWh (Figure 10), with p90 and p10 capacities of 624.4 and 746 TWh, respectively. The p50 for cavern number is 579, and the p90 and p10 for cavern number are 564 and 587 potential locations. The resulting geospatial distribution of the caverns differs from the site-specific depth model (4.4.1), as there are large gaps between the placed caverns (Figure 10). The caverns placed have a higher average capacity than the site-specific geological model (Layered Evaporite - Variable Cavern) 1.183 TWh vs .524 TWh (closest iteration to the p50 capacity of both models).
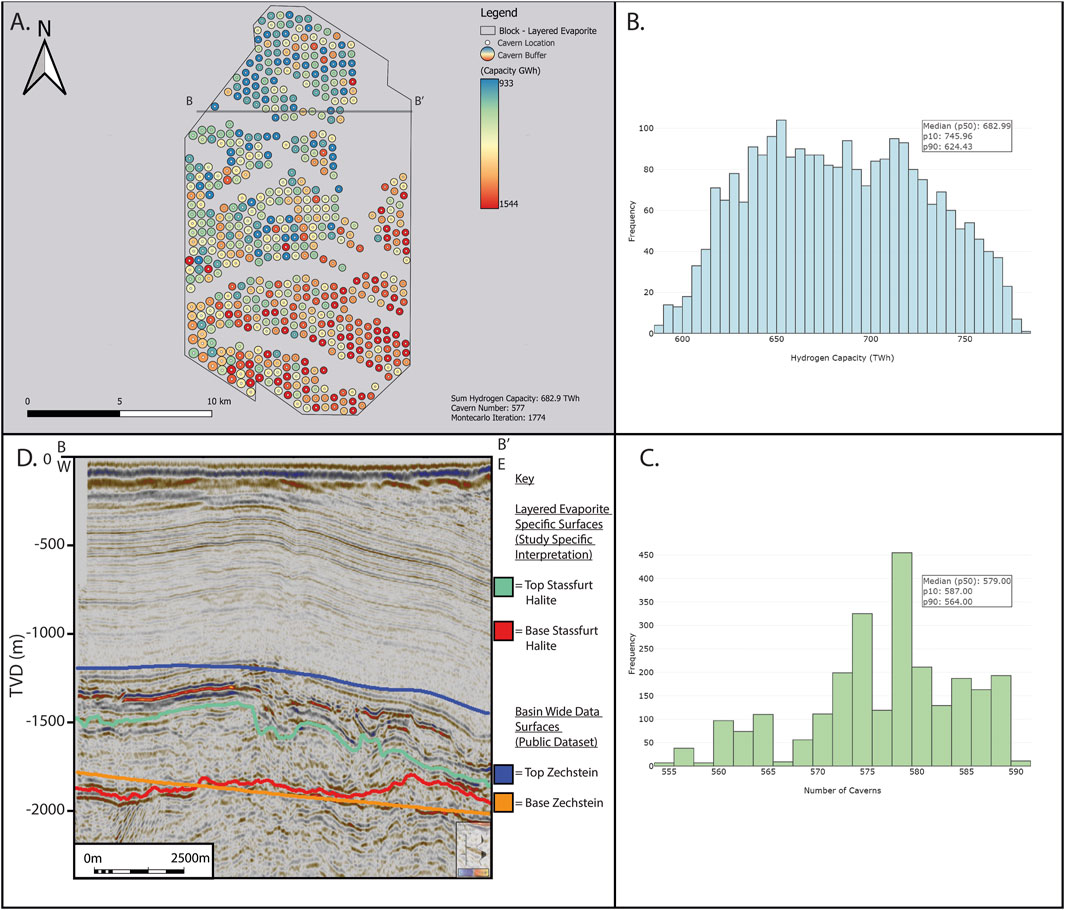
Figure 10. (A) Cavern placement map for the “Block Specific – Layered Evaporite’ AoI, variable cavern geometries using “Basin Wide” AoI depth surfaces. The geospatial placement represents the output model from the workflow with the total hydrogen capacity closest to the calculated p50 (Iteration 1774/2500). A total of 577 caverns are placed, with a sum of 682.9 TWh of hydrogen storage capacity. (B) Histogram of total hydrogen capacities for each iteration of the Montecarlo simulation (2500 iterations). (C) Histogram of the total number of caverns for each iteration of the Monte Carlo simulation (2500 iterations). (D) Seismic cross section running West to East, (B–B’) (Figures 1, 11A), in TVD (m). Stassfurt Halite surfaces interpreted from seismic survey MA933F002 and depth converted are present, Green (Top Stassfurt Halite) and Red (Base Stassfurt Halite/Top Basal Polyhalite). Blue and orange lines represent publicly available depth surfaces acquired from the NSTA of the top and base Zechstein, used for the “Basin Wide” AoI geological model.
Conceptual Cavern Cluster Developments
While the cumulative hydrogen capacity over large tracts of basins may be useful for an initial comparison of storage potential, a more useful consideration is the capacity of a salt cavern cluster development. We therefore considered five conceptual salt cavern cluster developments to demonstrate how the workflow could aid in early-stage planning of a possible cavern site at the project pre-feasibility stage (Figures 11A–E). The theoretical cluster concepts were developed using iteration 175 (Figure 8) from the Monte Carlo simulation, the iteration where the cumulative hydrogen capacity was closest to the p50 of the block specific–layered evaporite – variable cavern model (Layered Evaporite - Variable Cavern). We determined the following scenarios: 1) Maximum hydrogen storage capacity within a radius of 1.5 km from a fixed point; 2) Maximum hydrogen storage capacity within a cluster radius of 3 km from a fixed point; 3) Maximum cavern number within a radius of 1.5 km from a fixed point; 4) Maximum cavern number within a radius of 3 km from a fixed point; 5) Storage capacity within a radius of 1.5 km from pre-existing infrastructure (wellbore 41/05-1) (Figures 1, 4). Radiuses of 1.5–3 km are considered to be viable step-outs or deviation distances from a central facility point for the development of individual caverns based on known developments. The geographic layout of the development concepts is shown in Figure 11, and a summary of the results is in Table 2.
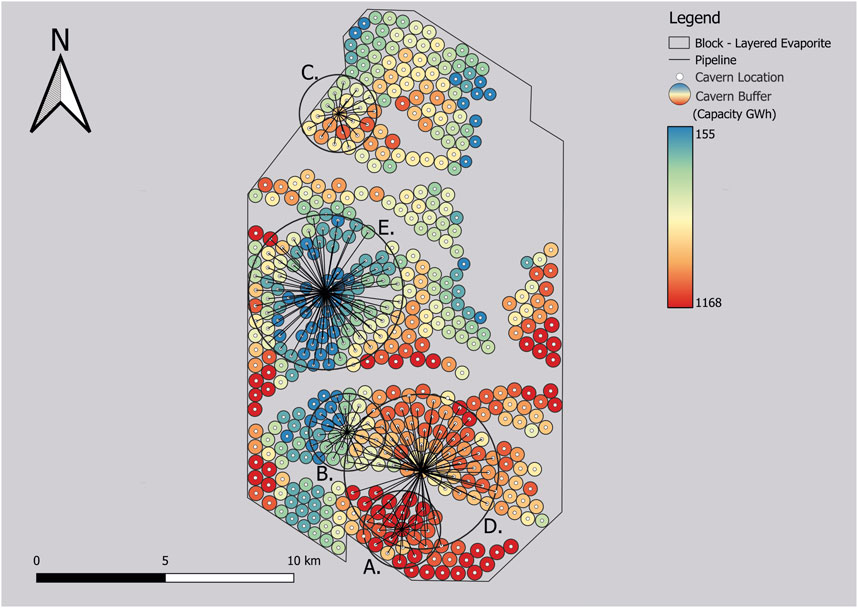
Figure 11. Salt cavern cluster concept play map. The base salt cavern map is the representative p50 of the “Block - Layered Evaporite” AoI variable cavern model (Figure 8B). 5 possible cavern cluster concepts are described (A) Maximum hydrogen capacity within a 1.5 km radius. (B) Maximum number of caverns within a 1.5 km radius. (C) 1.5 km radius placed on existing infrastructure (wellbore 41/05-1, Figures 1, 4). (D) Maximum hydrogen capacity within a 3 km radius. (E) Maximum cavern number within a 3 km radius. The radii were chosen to mimic offshore infrastructure.

Table 2. Theoretical salt cavern cluster information (Figure 11).
Sensitivity Analysis
The layered evaporite area cavern cluster’s largest uncertainty was the overburden gradient (Figure 12A), compared with the insolubility content for the salt wall area (Figure 12B). The layered evaporite area had a more constrained insolubility distribution (Figures 12A, B, Supplementary Appendix Table SD) than that of a salt wall and this is likely the cause for its lower sensitivity to insolubility content. The overburden pressure gradient was the most sensitive parameter for the layered evaporite area and the second for the salt wall, suggesting that more complex site-specific geomechanical models should be incorporated to help constrain the uncertainty in capacity estimates. The salt wall block was mostly insensitive to the depth uncertainty (Figure 12B), as increasing or decreasing the salt geometries did not change the suitability of an area for cavern emplacement; however, the layered evaporite area was sensitive (Figure 12A) to the depth uncertainty, probably due to the top salt being close to the maximum salt depth (Supplementary Appendix Table SB; Supplementary Appendix S6). Sensitivities for salt cavern emplacement will vary on a per-site basis as shown in Williams et al. (2022), with which our findings are consistent with.
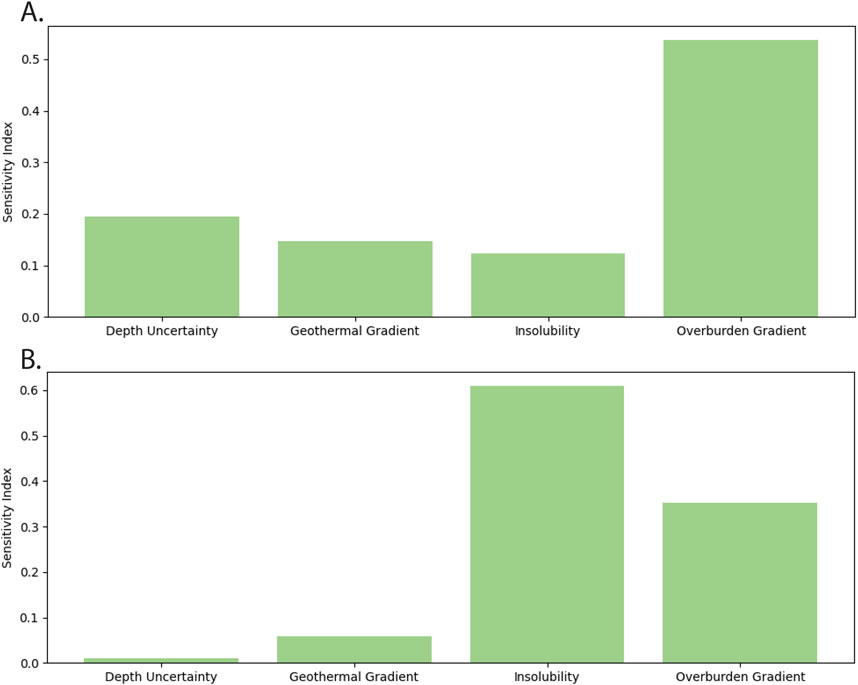
Figure 12. Sobol sensitivity results (Total sensitivity indices) of input parameters for (A) layered evaporite with variable caverns (4.3.2.1); and (B) The salt wall with variable caverns (4.3.1.1).
Discussion
Capacities and Volumetrics and Cavern Placement
The results described demonstrate the value of stochastic approaches to the evaluation of geological energy storage. The case studies demonstrate the importance of high-veracity geological models as inputs to such analysis. The results presented indicate that salt cavern capacity offshore could theoretically meet all existing scenarios for the UK’s hydrogen storage requirements, 40–115 TWh as suggested by the (Electricity System Operator, 2023) and (Cárdenas et al., 2021).
The basin-wide and sub-regional investigations demonstrated that there are up to 10,000s of TWh of potential storage within the Southern North Sea for hydrogen (Figures 5, 6), an order of magnitude greater than is required, and several times larger than the estimated working capacity of depleted gas fields and aquifers in the same location (2661 TWh) (Jahanbakhsh et al., 2024). The estimated p50 of possible cavern locations is 195,563 (Basin-Wide geological model) and 35,873 (Sub-Regional geological model), clearly providing a large number of possible sites for consideration for development in the future. When the total number of caverns is so high, the total capacity is largely irrelevant. The value of our Basin-wide and Sub-Regional results therefore does not come from hydrogen storage capacity, but rather from the cavern number and placement, both of which are required for energy system planning (Samsatli and Samsatli, 2019). At the block scale, results from the use of higher resolution geological models (Figures 7–11) demonstrated that areas equivalent to individual exploration and production licence areas (average 115 km2, largest 250 km2) the number of feasible cavern locations, and the total capacity are far greater than current scenarios for the hydrogen storage required in the UK (Cárdenas et al., 2021; Electricity System Operator, 2023).
By considering clusters of caverns (e.g., Figure 11) we made use of the spatial outputs of the model to compare the merits of different cluster development locations. We examined conceptual salt cavern cluster developments in the layered evaporite area, using the variable cavern Monte Carlo iteration closest to the p50 capacity value (Figures 8, 11) as the base case. The development concepts, while not incorporating integral detailed engineering constraints, were limited to spatial extents that were feasible with existing technologies (Energy Technologies Institute, 2013). The principal consideration is the step-out distance from a fixed offshore infrastructure point, for which we have considered distances of 1.5 km and 3 km. The distance from the fixed centre point to the centre of each theoretical cavern location was considered to be a viable representation of either a) a seabed pipeline distance to tie back individual caverns, or b) the drilling of a deviated well with a step-out. The examples shown are to demonstrate the value of the outputs from the workflow we have developed. Cavern cluster concept E (maximising for hydrogen capacity in a 3 km radius) had sufficient capacity to meet the minimum required energy storage set by Cárdenas et al. (2021), but this required a large number of caverns present >50. Cluster A, on the other hand, with 16.9 TWh potential made 42% of the 42 TWh requirement, with only 20 caverns and 22.3 km of pipeline (a typical salt cavern cluster development consists of up to 35 caverns; see Gillhaus, 2007).
Comparison to Other Studies
Previous studies have evaluated the offshore storage capacity of salt caverns in the Southern North Sea. We compared our results to these (Supplementary Appendix Table SE). Previous studies e.g., (Caglayan et al., 2020; Allsop et al., 2023) have suggested there is also greater than required energy storage capacity in both the onshore and offshore salt basin domains (43 TWh for 100% renewable penetration of the UK energy grid (Cárdenas et al., 2021)).
The results of our study are in line with those of Caglayan et al. (2020), which indicates there are thousands of TWh of potential storage within the offshore of the UK in the Southern North Sea, with the results of the two studies differing by only 6.7% in terms of total hydrogen capacity (Supplementary Appendix Table SE). Caglayan et al. (2020) only places cavern locations within 47 salt structures within the Southern North Sea, whereas our salt structure maps have 42 unique structures within our sub-regional depth model, which may account for the differences. These values suggest that the Southern North Sea’s capacity for LDES in salt caverns far exceeds any onshore basin within the UK (Supplementary Appendix Table SE), not considering the economic feasibility of offshore development.
While basin-wide capacity may be useful to benchmark one basin against another, all estimates demonstrate that the total of all possible cavern locations far exceeds the UK’s storage requirements (Supplementary Appendix Table SE). This is unsurprising as basin-wide estimates usually do not fully account for one of the most important factors, which is localised salt heterogeneities within the salt. For geographic areas with laterally extensive salt, the most pertinent issues are not related to total capacity, but rather to identifying the optimal geographic location of development clusters relative to other infrastructure (Sunny et al., 2020). Our workflow allowed for this geospatial investigation. This has implications for the development of energy production infrastructure, such as industrial clusters, marine renewable infrastructure and hydrogen production facilities, because the proximity of energy storage, production and usage is an important factor in considering whether sites next to each other can be advantageous (Walsh et al., 2023). It can also aid with identifying, for example, how many caverns can be placed in a suitable shallow offshore setting or within a set buffer distance from the previously mentioned infrastructure.
Sensitivity Analysis of Salt Cavern Site Capacity
The layered evaporite model was most sensitive to the overburden pressure gradient, while it was the second most sensitive parameter for the salt wall (Figure 12). This high level of sensitivity suggests that more complex site-specific geomechanical models should be incorporated to help reduce the uncertainty in site capacity estimates. The layered salt was less sensitive to insolubility than the salt wall; this is likely because the insoluble distribution of the layered salt was better constrained from the available data (Supplementary Appendix S4) than the insoluble distribution for the salt wall. The salt wall also had larger caverns placed due to the greater thickness available and as such, will be more negatively influenced by increased insoluble content. To reduce sensitivity to insoluble content refining the distribution with more data points or using seismic data for 3D quantitative interpretation of solubility content is essential to reduce uncertainty as the input distribution can change it substantially. The salt wall block was not sensitive to the depth uncertainty and hence bounding the top and base salt depths (Figure 12B), as increasing or decreasing the salt geometries did not change the suitability of an area for cavern placement, but the layered evaporite area was sensitive (Figure 12A) to the depth uncertainty, probably due to the top salt being close to the maximum salt depth (Supplementary Appendix Table SB, Supplementary Appendix S7). Sensitivities for salt cavern placement will vary on a per-site basis as shown in Williams et al. (2022), our findings agree with this and site-specific models for both insolubility and overburden pressures should be modelled to help confine capacity results.
Limitations of the Workflow/Approach
As with any subsurface modelling method, there are limitations. We used variable cavern geometries, and frequently the capacities were calculated to have volumes greater than those often reported in the literature (Supplementary Appendix Table SE). These volumes did not exceed the volume of the largest documented cavern, which has a total volume of 17,000,000 m3 (670 m high and 180 m diameter) (Leith, 2000). We compared the results of modifying the cavern geometries while keeping every other parameter the same, as shown in Supplementary Appendix Table SE (Layered evaporites – Variable Caverns - p50 vs layered evaporite – Fixed Caverns - p50 Models). Allowing for larger and variable cavern geometries allows for higher storage capacities within an area. However, there are fewer caverns placed within these iterations (Supplementary Appendix Table SE), if cavern placement was an important consideration, smaller caverns may be favoured as they allow for greater opportunities in their placement. Fewer, larger caverns would require less drilling to develop a possible cluster, although they would take a longer time to develop. It is also important to mention that within our workflow the cavern spacing remained static at twice the cavern diameter from the mid-point for all potential caverns; however, with increasing depth, the caverns will encounter higher associated stresses, and to account for this, a greater buffer distance may need to be incorporated into the workflow, reducing the potential cavern locations. While our geological models captured the thickness changes and the 3D structures of the Zechstein in the Southern North Sea, the model used a simple percentage for insoluble content and did not account for evaporite minerals that may be more soluble than halite (carnallite, for example) which may affect cavern morphology, nor did they incorporate a 3D model of the internal heterogeneities. For the layered evaporite area, however, we chose to take a 2D approach by mapping areas of non-viability such as faults and generalised areas of insolubility and removing them as deterministic non-viable areas. However, within the salt structures, insoluble stringers and complex geometries are typically associated with internal structural heterogeneity (Pichat, 2022). Imaging in salt structures is typically poor both due to the complex ray paths in the crystalline structure of salt, and because seismic surveys are often designed to image post and pre-salt (Jones and Davison, 2014). As such the 3D heterogeneity of the salt structures investigated was not incorporated into the workflow. Currently, the internal heterogeneity of salt units is one of the most important parameters to consider when planning a cavern site (Ramesh Kumar et al., 2021). Assuming pure halite rather than a heterogeneous evaporite system means that physical and rock mechanical properties will be incorrectly calculated, compromising the longevity of the salt cavern within the salt body. Several new methods of seismic imaging and depth conversion can offer substantially improved images of the internal workings of salt units (Multi-layer pre-stack depth migration (PSDM), Full Waveform Inversion (FWI)). It is imperative that future workflows focusing on a more potential site investigation scale, include the estimation and 3D spatial understanding of intra-salt heterogeneities.
Evaporite units are known to cause thermal anomalies in subsurface heat flow due to their crystalline structure, which conducts thermal energy more efficiently than the surrounding lithologies (Jackson and Hudec, 2017). This increased complexity makes the use of a geothermal gradient a simplification for basins with extensive salt (Williams et al., 2022), and future work could investigate the value of incorporating 1D, 2D or 3D heat flow models to determine the influence of salt layers on thermal structure. The flexibility of our workflow means that the outputs of such modelling could be incorporated in the future.
The geomechanics of cavern emplacement were not considered in detail in our workflow. The distances used for geomechanical stability between caverns were taken from the literature and determined to be suitable for our workflow development (Allen et al., 1982; Caglayan et al., 2020). It should be noted that caverns emplaced deeper may require larger separating buffer distances as there are higher stresses acting upon them, and increased distances between caverns would reduce the total cavern number and hence the total capacity within an area (Williams et al., 2022). Area-specific geomechanical models could be incorporated into our workflow for more suitable cavern placement, such as rheological contrast between evaporitic and non-evaporitic units, but the development of such models was beyond the scope of our research.
Despite these limitations, the workflow has been designed to be easily modified for different geological models, parameters, or uncertainties. This is seen by the number of different cases and iterations we have run, where the inputs to the workflow have been modified to better match the input geological model. The outputs can even be modelled to plot against the initial 3D seismic data from which the depth surfaces are derived, allowing for visualisation of the true placement location (Supplementary Appendix S8).
Veracity of Data
The necessity for geological models to be reliable and reproducible is essential where they underpin key developments as part of sustainable pathways and in achieving Net Zero (Steventon et al., 2022). We compared the layered evaporite salt model using seismic specific data (Layered Evaporite - Variable Cavern; Figure 8) and basin-wide depth data (Layered Evaporite - Basin Wide Depth Model – Variable Cavern; Figure 10). Both models use the same parameters with only the surfaces and associated depth uncertainty changing (Supplementary Appendix S7). Changing the surfaces caused several parameters to be affected: 1) formation thickness changed because the basin-wide data were derived from top to base Zechstein, whereas the site-specific surfaces were derived from top to base Stassfurt Halite (Figure 4). 2) The depth to the top salt was different, with the basin-wide model being shallower, allowing for more potential locations. 3) The grid cell resolution was also different; Supplementary Appendix S7 shows the differences in surfaces. The basin wide data results estimated 75 more caverns, 419 TWh more capacity, and an average cavern working capacity of 0.658 TWh greater than the specific data geological model. These differences arise from the basin-wide data use of the top and base Zechstein as input, rather than having the specified salt target, which in turn caused the salt to be thicker, allowing for larger caverns to be placed through the workflow. Using the top and base Zechstein also resulted in insoluble stratigraphic layers within the Zechstein, such as the Plattendolomit (Figures 2–4) being within the area for cavern emplacement in the workflow. The compositional heterogeneity of evaporites and in particular insoluble lithologies, such as the Plattendolomit, has the potential to cause issues, such as interbed collapse (and associated loss of volume due to volume occupied by insoluble contents within the cavern sump), contamination, or act as a porous and permeable pathway for hydrogen to escape, and, as such should be avoided where possible (Chen et al., 2018; Zhang et al., 2021; Yang et al., 2023; Zhu et al., 2023).
The public surfaces are also of lower resolution with a grid cell spacing of 250 m, as opposed to 50 m. This lower resolution leads to ineffective packing of the caverns (Figure 10A), as the grid cell size is greater than the typical buffer (∼100 m) between adjacent caverns. A higher resolution model not only enabled more potential cavern locations to be considered but also captured a higher resolution of structural variability in the geometry of the salt interval. The work presented here suggests that the minimum grid cell size of the input geological model is at most 4 times the minimum cavern size diameter, as this allows each grid cell to have a point with minimal overlap. At lower resolutions the cavern packing is not efficiently modelled (Supplementary Appendix S9). At higher grid cell resolutions, it is possible to model more cavern locations and then determine the optimum cavern spacing and placement (Supplementary Appendix S9).
Importance of Reproducibility and Replicability
Within the subsurface geosciences, practical frameworks for reproducibility are in their infancy, particularly where there are significant uncertainties associated with the data (Steventon et al., 2022). It has been identified that the availability of data and software (including code), frequently limits the ability to reproduce studies (Ireland et al., 2023). Previous studies of geological energy storage estimates rarely provide all the information required for reproduction. This study has made the code available through a CC BY-SA so that it can be used, revised, and modified, including for commercial purposes. This therefore allows others to reproduce our work (same method, same data) and to replicate our work (same method, different data). In addition to the method, it is vital that the underlying data for studies are made available and easily accessible (Hardwicke et al., 2018). Previous studies of geological energy storage have not always provided accessible data repositories with sufficient data to examine the reliability of capacity estimates (different methods, same data). In this study we used data and interpretations from existing open-licence sources (NSTA), as well as our own interpretations, which we also made available through a CC-Y licence. This approach allows for the evaluation of the reproducibility and reliability of our findings.
The comparison shown in Supplementary Appendix Table SE highlights the importance of reproducibility and reliability in studies where results may have implications for both the scientific community and policymakers. The results of Caglayan et al. (2020) and Allsop et al. (2023), for the same areas showed differences of up to 685 TWh and 9393 TWh respectively (compared with the sub-regional model). With such large differences in predictions, it is important to be able to understand where such differences arise from; however, replicability is only viable when the input data to a model are made available and accessible. While our capacity calculations were larger than those proposed by Caglayan et al. (2020), they are in general agreement (generalisable, different method, different data) that there are over 9000 TWh of storage potential of hydrogen in the Southern North Sea, with our sub-regional model differing by 6.7%, while using different subsurface datasets (Caglayan et al. (2020) did not incorporate layered evaporite domains in their geological model). Allsop et al. (2023) estimated significantly different capacities in comparison to this study, both for the salt wall and the area of the sub-regional model (Supplementary Appendix Table SB, E) while using the same seismic data (2016 Southern North Sea Mega-merge). They estimated that there are only 1485 cavern locations within the sub-regional area, as opposed to the 36,466 in our study, and only 105 within the Audrey salt wall as opposed to the 1154 in our study (using the same cavern geometries) (Figures 6, 7). Unfortunately, due to the lack of detail in the methodology and results presented (no geospatial data regarding cavern placement) in addition to the lack of data being provided in the data repository by Allsop et al. (2023) we were unable to reproduce their results and make a detailed comparison between each workflow to understand where these differences originated. This example of researchers reaching different conclusions while utilising the same dataset emphasises both the importance of reproducibility and replicability in geosciences, adding to the many studies in the geoscience community, where the results cannot be reproduced or replicated (Ireland et al., 2023). The differences also emphasise the importance of using the same parameters within the methodology, the use or omission of essential parameters such as intra-salt heterogeneities, can significantly alter the number of potential caverns. Another important aspect is the veracity of the interpretation obtained from the same dataset as this will have a strong influence on the geological model and therefore on the results. When all aspects of research are open this will improve their trustworthiness (Rosman et al., 2022), which is essential if the findings are to inform policy or aspects of national planning, such as energy systems (UK Government, 2012). While much of the research in this field, particularly block/licence-scale evaluations, may use proprietary data, technologies and interpretations, efforts should be made to make the data and information open where possible.
Energy System Integration
The outputs generated from our workflow are such that they contain individual cavern locations, specifications, and capacities. These outputs can be used as inputs to further energy system modelling that includes storage (see Sunny et al., 2020). While energy system modelling and energy value chain studies include offshore energy generation in their models, they typically implement storage opportunities in the onshore domain rather than offshore (mainly due to economic feasibility), limiting opportunities and limiting exploration of possible solutions (Samsatli and Samsatli, 2019). Our results can aid in the design of energy systems at all scales (from national grid level planning to local energy storage requirements) because of the different scales of geological models that have gone through our workflow (from broad, whole basin geological models to site-specific models). While we are not suggesting the integration of every potential cavern location generated into an energy system, the results allow for areas with high hydrogen supply potential and LDES demand to be located and utilised.
The geographic results, both individual caverns and conceptual clusters can be reviewed with respect to important energy infrastructure. For example, Figure 13 shows the number of caverns and capacity within a 20 km radius of existing and planned offshore wind developments in the Southern North Sea. Of the 32 developments, 15 have >1000 potential cavern locations and 13 have over 500 TWh of potential hydrogen capacity (Figure 13). We can also examine the setting of the cavern locations, such as water depth or distance from the coastline, both of which could impact development costs (Energy Technologies Institute, 2013). All cavern locations are situated at a depth of less than 100 m, which would mean they could be accessed by a jack-up rig (the typical limit is 120 m). There are 22,000 possible cavern locations within 10 km and 37,000 within 20 km of the east coast (Basin wide model).
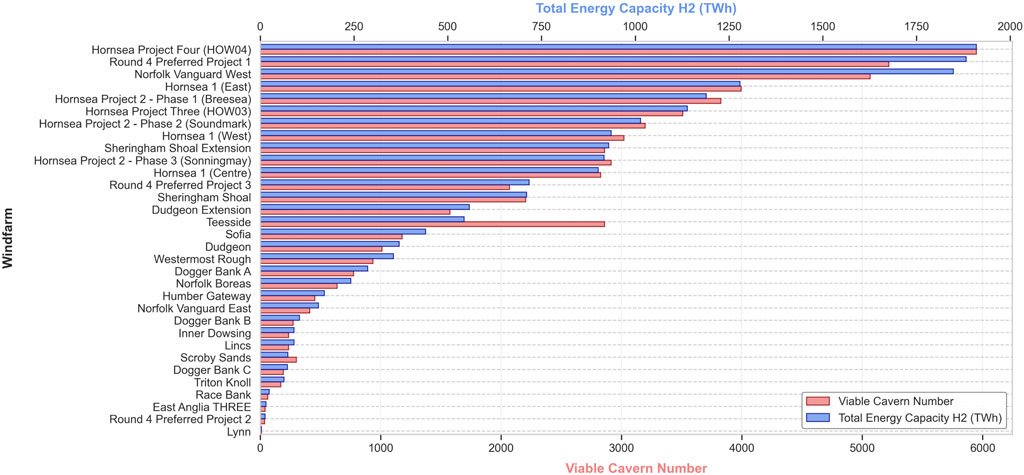
Figure 13. Wind farms located within the “Basin Wide” AoI (Figure 5), plotted against the potential number of caverns and total hydrogen storage capacity within a 20 km buffer of the wind farm site [Basin Wide results used (Basin Wide – Fixed caverns)].
These are some possible examples of how the results from this study and our workflow could be integrated into energy system design. While our brief overview of this is simplistic, our data could be used for much more complex analysis because of the level of information associated with each cavern generated.
Offshore Salt Caverns for LDES
To date, all salt caverns have been emplaced onshore, but offshore salt cavern projects have been proposed before (Evans and Holloway, 2009). We have demonstrated that not only does the estimated total available capacity exceed current estimates for storage but that the number of potential geographic locations offshore has the potential to provide effective integration with current and future marine renewable infrastructure (Figures 5, 6, 13) and to meet the calculated demand (43 TWh) (Cárdenas et al., 2021).
The integration of salt cavern clusters for LDES could provide greater flexibility and variability in offshore renewable energy production (Arellano-Prieto et al., 2022). However, the offshore development costs such as drilling, tie-in and pipeline costs, of such infrastructure need to be considered as to whether they are economically viable for these areas, specifically the idealised locations for caverns that are next to hydrogen production hubs (generating either blue or green hydrogen). Integrating all aspects of hydrogen production will allow for the optimisation of the integration, flexibility and transport of hydrogen from production to storage (Walsh et al., 2023).
Offshore energy infrastructure has costs associated with it that are higher than those that occur onshore, for example, wind turbines are 50% more expensive offshore than onshore (Bilgili et al., 2011). Savings may be possible with salt caverns, as the brine produced by the creation of the salt caverns can be sold to reduce costs or, if not possible, diluted and disposed of at sea, which is more cost-effective than the cost of transporting the brine onshore (Ahmad and Baddour, 2014). The cost of pipelines, drilling and tie-in costs will be a key aspect of the site consideration as they will be a significant component of the CAPEX costs. For all our theoretical salt cavern sites, we have modelled the possible pipeline distances for a single cluster to provide reasonable estimates of what may be required (Table 2), but a more thorough specific investigation into this will be needed.
Conflict of spatial interests remains a factor that needs to be considered when planning any offshore infrastructure, especially for a basin with high renewable potential, such as the North Sea (Guşatu et al., 2024). Any infrastructure, such as windfarms, LDES, or CCS requires space with suitable buffers around it to ensure safe operation without causing interference with the operations of other offshore projects. As such, areas that we have described as having potential for salt cavern emplacement may no longer be suitable due to areas being prioritised for other technologies. However, the large number of potential cavern sites 199,489 (Figure 5) and the relatively small number needed to meet the storage requirements (Table 2) suggest that this issue may not affect the location of cavern placement.
Alternative energy vectors could be stored in salt caverns to alleviate carbon emissions in other industries. Global shipping accounts for 2% of global carbon dioxide emissions, and both ammonia and methanol have been suggested as alternative zero-emission fuel sources (Svanberg et al., 2018; Gallucci, 2021). Ammonia is a possible energy vector alternative (Patonia and Poudineh, 2020). At the average internal pressure/temperature conditions of the salt caverns in our basin-wide study (64°C and 36.2 MPa), ammonia would be in its supercritical phase and methanol would be in its liquid phase (National Institute of Standards and Technology, 2023). Ammonia has previously been suggested as storable in salt caverns (Adams and Cottle, 1954). The combination of storage and offshore production of these low-emission fuels would allow for a fully integrated and green, ship refuelling ecosystem.
Conclusion
In this paper we have demonstrated our proposed workflow using several geological models and parameters. We position this workflow at the pre-feasibility stage of an area for the investigation placement of salt caverns. The workflow takes a geological model as an input and outputs valid salt cavern locations along with capacity estimates. The workflow has been designed so that all parameters and variables can be changed to suit the geological model and the area of interest, even allowing the chosen energy vector to be altered. The workflow allows for the input of not only deterministic values but stochastic values, thus compensating for the uncertainty typically associated with geological models of the subsurface.
With our workflow we have produced realistic theoretical salt cavern clusters that help to show how the results from our model could be used to develop such a cluster. The capacity results showed that a single large offshore cavern cluster (with a 3 km diameter AOI) could have enough hydrogen storage capacity to meet the UK’s long-term energy storage requirements in full. The workflow and associated data should be used to aid site planners or policymakers in making further decisions regarding offshore hydrogen storage using salt caverns.
The offshore domain is often not considered when deciding where LDES should be placed. We have demonstrated that the UK offshore is a suitable location, with over 199,000 cavern locations and +10,000 TWh of hydrogen capacity. This viability opens up the possibility of co-location with offshore energy production hubs, allowing for the UK to have a fully green energy production hub operating offshore.
We have also compared our results with other studies to emphasise how important it is to have a reproducible and replicable methodology. All code, data and interpretations used in this study have been provided within the data repository.
The workflow presented addresses some of the main parameters that need to be assessed and considered during basin screening and initial planning of UES in salt basins and areas of interest. However, more detailed geological information obtained from well data combined with high-resolution seismic data derived from PSDM models, such as salt heterogeneities and internal structuring and composition, needs to be considered and incorporated in detail when moving from the conceptual stage to the effective planning of salt cavern infrastructure.
Data Availability Statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://data.ncl.ac.uk/projects/Capturing_geological_uncertainty_in_salt_cavern_developments_for_hydrogen_storage_Case_study_from_Southern_North_Sea_DATA_REPO/186837. Seismic and well data were provided by the North Sea Transition Authority under an Open Government Licence. Bathymetric data were provided by The European Marine Observation and Data Network.
Author Contributions
HB–Conceptualisation, data curation, analysis, methodology, data manipulation, data visualisation, writing original + review and editing, project administration; MI–Supervision, conceptualisation, writing original + review and editing, funding, conceptualisation; CL–Supervision, review and editing. All authors contributed to the article and approved the submitted version.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. HB’s PhD is funded by the Centre for Doctoral Training (CDT) in Geoscience and the Low Carbon Energy Transition.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We acknowledge and are grateful to the SLB for providing academic licences for their Petrel and Techlog software which was used to visualise and interrogate the seismic data. We would also like to thank the reviewers whose comments and feedback greatly improved this paper.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.escubed.org/articles/10.3389/esss.2024.10125/full#supplementary-material
Footnotes
1https://opendata-nstauthority.hub.arcgis.com/explore
References
Ahmad, N., and Baddour, R. E. (2014). A Review of Sources, Effects, Disposal Methods, and Regulations of Brine into Marine Environments. Ocean & Coast. Manag. 87, 1–7. doi:10.1016/j.ocecoaman.2013.10.020
Al-Chalabi, M. (2014). Principles of Seismic Velocities and Time-To-Depth Conversion. Houten: EAGE Publications.
Allen, K. (1971). Eminence Dome - Natural-Gas Storage in Salt Comes of Age. J. Petroleum Technol. 24 (11), 1299–1301. doi:10.2118/3433-pa
Allen, P. A., and Allen, J. R. (2013). Basin Analysis: Principles and Application to Petroleum Play Assessment. Wiley-Blackwell.
Allen, R. D., Doherty, T. J., and Thorns, R. L. (1982). Geotechnical Factors and Guidelines for Storage of Compressed Air in Solution Mined Salt Cavities.
Allsop, C., Yfantis, G., Passaris, E., and Edlmann, K. (2023). Utilizing Publicly Available Datasets for Identifying Offshore Salt Strata and Developing Salt Caverns for Hydrogen Storage. Geol. Soc. Lond. Spec. Publ. 528 (1), 139–169. doi:10.1144/sp528-2022-82
Alyafei, N. (2021). Fundamentals of Reservoir Rock Properties - 2nd Edition. Doha, Qatar: Hamad bin Khalifa University Press. doi:10.5339/Fundamentals_of_Reservoir_Rock_Properties_2ndEdition
Arellano-Prieto, Y., Chavez-Panduro, E., Salvo Rossi, P., and Finotti, F. (2022). Energy Storage Solutions for Offshore Applications. Energies 15 (17), 6153. doi:10.3390/en15176153
Barnett, H., Ireland, M., and van der Land, C. (2024). Capturing Geological Uncertainty in Salt Cavern Developments for Hydrogen 1 Storage: Case Study from Southern North Sea. EarthArXiv. doi:10.31223/x5pq4c
Barnett, H. G., Ireland, M. T., and van der Land, C. (2023). Characterising the Internal Structural Complexity of the Southern North Sea Zechstein Supergroup Evaporites. Basin Res. 35 (5), 1651–1673. doi:10.1111/bre.12768
Bauer, S., Beyer, C., Dethlefsen, F., Dietrich, P., Duttmann, R., Ebert, M., et al. (2013). Impacts of the Use of the Geological Subsurface for Energy Storage: An Investigation Concept. Environ. Earth Sci. 70 (8), 3935–3943. doi:10.1007/s12665-013-2883-0
Bérest, P., Brouard, B., Hévin, G., and Réveillère, A. (2021). Tightness of Salt Caverns Used for Hydrogen Storage. 55th U.S. Rock Mechanics/Geomechanics Symp.
Bilgili, M., Yasar, A., and Simsek, E. (2011). Offshore Wind Power Development in Europe and its Comparison With Onshore Counterpart. Renew. Sustain. Energy Rev. 15 (2), 905–915. doi:10.1016/j.rser.2010.11.006
Bourke, L., Delfiner, P., Felt, T., Grace, M., Luthi, S., Serra, O., et al. (1989). Using Formation Microscanner Images: The (Schlumberger) Technical Review. 16–40.
Caglayan, D. G., Weber, N., Heinrichs, H. U., Linßen, J., Robinius, M., Kukla, P. A., et al. (2020). Technical Potential of Salt Caverns for Hydrogen Storage in Europe. Int. J. Hydrogen Energy 45 (11), 6793–6805. doi:10.1016/j.ijhydene.2019.12.161
Calado, G., and Castro, R. (2021). Hydrogen Production From Offshore Wind Parks: Current Situation and Future Perspectives. Appl. Sci. 11 (12), 5561. doi:10.3390/app11125561
Cárdenas, B., Swinfen-Styles, L., Rouse, J., Hoskin, A., Xu, W., and Garvey, S. D. (2021). Energy Storage Capacity vs. Renewable Penetration: A Study for the UK. Renew. Energy 171, 849–867. doi:10.1016/j.renene.2021.02.149
Centrica (2023). Centrica Bolsters UK’s Energy Security by Doubling Rough Storage Capacity. Available at: https://www.centrica.com/media-centre/news/2023/centrica-bolsters-uk-s-energy-security-by-doubling-rough-storage-capacity/.
Chen, X., Li, Y., Liu, W., Ma, H., Ma, J., Shi, X., et al. (2018). Study on Sealing Failure of Wellbore in Bedded Salt Cavern Gas Storage. Rock Mech. Rock Eng. 52 (1), 215–228. doi:10.1007/s00603-018-1571-5
Costa, P. V. M., Costa, A. M., Szklo, A., Branco, D. C., Freitas, M., and Rosa, L. P. (2017). UGS in Giant Offshore Salt Caverns to Substitute the Actual Brazilian NG Storage in LNG Vessels. J. Nat. Gas Sci. Eng. 46, 451–476. doi:10.1016/j.jngse.2017.06.035
Crotogino, F., Schneider, G.-S., and Evans, D. J. (2017). Renewable Energy Storage in Geological Formations. Proc. Institution Mech. Eng. Part A J. Power Energy 232 (1), 100–114. doi:10.1177/0957650917731181
Doornenbal, J. C., Kombrink, H., Bouroullec, R., Dalman, R. A. F., De Bruin, G., Geel, C. R., et al. (2019). New Insights on Subsurface Energy Resources in the Southern North Sea Basin Area. London, England: Geological Society, London, Special Publications. doi:10.1144/sp494-2018-178
Dowling, J. A., Rinaldi, K. Z., Ruggles, T. H., Davis, S. J., Yuan, M., Tong, F., et al. (2020). Role of Long-Duration Energy Storage in Variable Renewable Electricity Systems. Joule 4 (9), 1907–1928. doi:10.1016/j.joule.2020.07.007
Eising, J., Brouwer, F., and Bernd, A. (2021). Appendix: Risk Analysis of Worldwide Salt Cavern Storage Vrije Universiteit Amsterdam.
Elam, S. D. (2007). First Gas After 40 Years – The Geophysical Challenges of the Saturn Gas Complex AAPG Annual Convention 2007. Claifornia: Long Beach.
Electricity System Operator (2023). Future Energy Scenarios. Available at: https://www.nationalgrideso.com/document/283101/download.
Energy Technologies Institute (2013). Hydrogen Storage and Flexible Turbine Systems WP2 Report – Hydrogen Storage Carbon Capture and Storage - Hydrogen Turbines, Issue.
Evans, D. J. (2007). An Appraisal of Underground Gas Storage Technologies and Incidents, for the Development of Risk Assessment Methodology. B. G. Surv.
Evans, D. J., and Holloway, S. (2009). A Review of Onshore UK Salt Deposits and Their Potential for Underground Gas Storage. Geol. Soc. Lond. Spec. Publ. 313 (1), 39–80. doi:10.1144/sp313.5
Fanchi, J. R., and Christiansen, R. L. (2016). Properties of Reservoir Fluids. In Introduction to Petroleum Engineering. 45–66. doi:10.1002/9781119193463.ch3
François, L. L. (2021). Four Ways to Store Large Quantities of Hydrogen Abu Dhabi International Petroleum Exhibition & Conference. Abu Dhabi, UAE.
Fyfe, L.-J. C., and Underhill, J. R. (2023). A Regional Geological Overview of the Upper Permian Zechstein Supergroup (Z1 to Z3) in the Sw Margin of the Southern North Sea and Onshore Eastern England. J. Petroleum Geol. 46 (3), 223–256. doi:10.1111/jpg.12837
Gallucci, M. (2021). The Ammonia Solution: Ammonia Engines and Fuel Cells in Cargo Ships Could Slash Their Carbon Emissions. IEEE Spectr. 58, 44–50. doi:10.1109/mspec.2021.9370109
Glennie, K. W. (1998). Petroleum Geology of the North Sea: Basic Concepts and Recent Advances 4 ed. London, England: Blackwell Scoence. doi:10.1002/9781444313413
Grant, R. J., Underhill, J. R., Hernández-Casado, J., Barker, S. M., and Jamieson, R. J. (2019). Upper Permian Zechstein Supergroup Carbonate-Evaporite Platform Palaeomorphology in the UK Southern North Sea. Mar. Petroleum Geol. 100, 484–518. doi:10.1016/j.marpetgeo.2017.11.029
Guşatu, L. F., Zuidema, C., Faaij, A., Martínez-Gordón, R., and Santhakumar, S. (2024). A Framework to Identify Offshore Spatial Trade-Offs in Different Space Allocation Options for Offshore Wind Farms, as Part of the North Sea Offshore Grid. Energy Rep. 11, 5874–5893. doi:10.1016/j.egyr.2024.05.052
Hardwicke, T. E., Mathur, M. B., MacDonald, K., Nilsonne, G., Banks, G. C., Kidwell, M. C., et al. (2018). Data Availability, Reusability, and Analytic Reproducibility: Evaluating the Impact of a Mandatory Open Data Policy at the Journal Cognition. R. Soc. Open Sci. 5 (8), 180448. doi:10.1098/rsos.180448
Hassanpouryouzband, A., Adie, K., Cowen, T., Thaysen, E. M., Heinemann, N., Butler, I. B., et al. (2022). Geological Hydrogen Storage: Geochemical Reactivity of Hydrogen With Sandstone Reservoirs. ACS Energy Lett. 7 (7), 2203–2210. doi:10.1021/acsenergylett.2c01024
Heinemann, N., Alcalde, J., Miocic, J. M., Hangx, S. J. T., Kallmeyer, J., Ostertag-Henning, C., et al. (2021). Enabling Large-Scale Hydrogen Storage in Porous Media – The Scientific Challenges. Energy & Environ. Sci. 14 (2), 853–864. doi:10.1039/d0ee03536j
Heinemann, N., Booth, M. G., Haszeldine, R. S., Wilkinson, M., Scafidi, J., and Edlmann, K. (2018). Hydrogen Storage in Porous Geological Formations – Onshore Play Opportunities in the Midland Valley (Scotland, UK). Int. J. Hydrogen Energy 43 (45), 20861–20874. doi:10.1016/j.ijhydene.2018.09.149
Herman, J., and Usher, W. (2017). SALib: An Open-Source Python Library for Sensitivity Analysis. J. Open Source Softw. 2 (9), 97. doi:10.21105/joss.00097
Hunter, C. A., Penev, M. M., Reznicek, E. P., Eichman, J., Rustagi, N., and Baldwin, S. F. (2021). Techno-Economic Analysis of Long-Duration Energy Storage and Flexible Power Generation Technologies to Support High-Variable Renewable Energy Grids. Joule 5 (8), 2077–2101. doi:10.1016/j.joule.2021.06.018
HyUnder (2013). D3.1 - Assessment of the Potential, the Actors and Relevant Business Cases for Large Scale and Seasonal Storage of Renewable Electricity by Hydrogen Underground Storage in Europe.
Ireland, M., Algarabel, G., Steventon, M., and Munafò, M. (2023). How Reproducible and Reliable Is Geophysical Research? Seismica 2 (1). doi:10.26443/seismica.v2i1.278
Iwanaga, T., Usher, W., and Herman, J. (2022). Toward SALib 2.0: Advancing the Accessibility and Interpretability of Global Sensitivity Analyses. Socio-Environmental Syst. Model. 4, 18155. doi:10.18174/sesmo.18155
Jackson, M. P. A., and Hudec, M. R. (2017). Salt Tectonics. Cambridge University Press. doi:10.1017/9781139003988
Jahanbakhsh, A., Louis Potapov-Crighton, A., Mosallanezhad, A., Tohidi Kaloorazi, N., and Maroto-Valer, M. M. (2024). Underground Hydrogen Storage: A UK Perspective. Renew. Sustain. Energy Rev. 189, 114001. doi:10.1016/j.rser.2023.114001
Johnson, W.Stoker (1993). Lithostratigraphic Nomenclature of the UK North Sea: Permian and Triassic of the Southern North Sea V. 6. Br. Geol. Surv.
Jones, I. F., and Davison, I. (2014). Seismic Imaging in and Around Salt Bodies. Interpretation 2 (4), SL1–SL20. doi:10.1190/int-2014-0033.1
King, M., Jain, A., Bhakar, R., Mathur, J., and Wang, J. (2021). Overview of Current Compressed Air Energy Storage Projects and Analysis of the Potential Underground Storage Capacity in India and the UK. Renew. Sustain. Energy Rev. 139, 110705. doi:10.1016/j.rser.2021.110705
Kueppers, M., Paredes Pineda, S. N., Metzger, M., Huber, M., Paulus, S., Heger, H. J., et al. (2021). Decarbonization Pathways of Worldwide Energy Systems – Definition and Modeling of Archetypes. Appl. Energy 285, 116438. doi:10.1016/j.apenergy.2021.116438
Landinger, H., and Crotogino, F. (2007). The Role of Large-Scale Hydrogen Storage for Future Renewable Energy Utilisation. Second International Renewable Energy Storage Conference (IRES II).
Leith, W. (2000). Geologic and Engineering Constraints on the Feasibility of Clandestine Nuclear Testing by Decoupling in Large Underground Cavities. doi:10.3133/ofr0128
Lokhorst, A., and Wildenborg, T. (2006). Introduction on CO2 Geological Storage - Classification of Storage Options. Oil & Gas Sci. Technol. 60 (3), 513–515. doi:10.2516/ogst:2005033
Lord, A. s. (2009). Overview of Geologic Storage of Natural Gas with an Emphasis on Assessing the Feasibility of Storing Hydrogen.
Ma, H., Wei, X., Shi, X., Liang, X., Bai, W., and Ge, L. (2022). Evaluation Methods of Salt Pillar Stability of Salt Cavern Energy Storage. Energies 15 (20), 7570. doi:10.3390/en15207570
McNamara, J. W., DeAngelis, V., Byrne, R. H., Benson, A., Chalamala, B. R., and Masiello, R. (2022). Long-duration Energy Storage in a Decarbonized Future: Policy Gaps, Needs, and Opportunities. MRS Energy & Sustain. 9 (2), 142–170. doi:10.1557/s43581-022-00037-9
Muhammed, N. S., Haq, B., Al Shehri, D., Al-Ahmed, A., Rahman, M. M., and Zaman, E. (2022). A Review on Underground Hydrogen Storage: Insight into Geological Sites, Influencing Factors and Future Outlook. Energy Rep. 8, 461–499. doi:10.1016/j.egyr.2021.12.002
National Institute of Standards and Technology (2023). National Institute of Standards and Technology. Maryland, United States: U.S Department of Commerce.
North Sea Transition Authority (2022). Gas Storage and Unloading. Available at: https://www.nstauthority.co.uk/regulatory-information/gas-storage-and-unloading/#:∼:text=Award%20of%20Gas%20Storage%20Licence%20%2D%20July%202022,in%20the%20Southern%20North%20Sea.
Oil and Gas Authority (2021). OGA Stratergy. Available at: https://www.nstauthority.co.uk/media/7105/the-oga-strategy.pdf.
Ozarslan, A. (2012). Large-scale Hydrogen Energy Storage in Salt Caverns. Int. J. Hydrogen Energy 37 (19), 14265–14277. doi:10.1016/j.ijhydene.2012.07.111
Parkes, D., Evans, D. J., Williamson, P., and Williams, J. D. O. (2018). Estimating Available Salt Volume for Potential CAES Development: A Case Study Using the Northwich Halite of the Cheshire Basin. J. Energy Storage 18, 50–61. doi:10.1016/j.est.2018.04.019
Patonia, A., and Poudineh, R. (2020). Ammonia as a Storage Solution for Future Decarbonized Energy Systems. OIES Pap. El.
Peryt, T., Geluk, M., Mathiesen, M., Paul, J., and Smith, K. (2010). “Chapter 8 Zechstein,” in Petroleum Geological Atlas of the South Permian Basin Area
Pichat, A. (2022). Stratigraphy, Paleogeography and Depositional Setting of the K–Mg Salts in the Zechstein Group of Netherlands—Implications for the Development of Salt Caverns. Minerals 12 (4), 486. doi:10.3390/min12040486
Raith, A., Strozyk, F., Visser, J., and Urai, J. (2016). Evolution of Rheologically Heterogeneous Salt Structures: A Case Study From the NE Netherlands. Solid earth. 7 (1), 67–82. doi:10.5194/se-7-67-2016
Ramesh Kumar, K., Makhmutov, A., Spiers, C. J., and Hajibeygi, H. (2021). Geomechanical Simulation of Energy Storage in Salt Formations. Sci. Rep. 11 (1), 19640. doi:10.1038/s41598-021-99161-8
Rosman, T., Bosnjak, M., Silber, H., Koßmann, J., and Heycke, T. (2022). Open Science and Public Trust in Science: Results from Two Studies. Public Underst. Sci. 31 (8), 1046–1062. doi:10.1177/09636625221100686
Samsatli, S., and Samsatli, N. J. (2019). The Role of Renewable Hydrogen and Inter-seasonal Storage in Decarbonising Heat – Comprehensive Optimisation of Future Renewable Energy Value Chains. Appl. Energy 233-234, 854–893. doi:10.1016/j.apenergy.2018.09.159
Sepulveda, N. A., Jenkins, J. D., Edington, A., Mallapragada, D. S., and Lester, R. K. (2021). The Design Space for Long-Duration Energy Storage in Decarbonized Power Systems. Nat. Energy 6 (5), 506–516. doi:10.1038/s41560-021-00796-8
Shan, R., Reagan, J., Castellanos, S., Kurtz, S., and Kittner, N. (2022). Evaluating Emerging Long-Duration Energy Storage Technologies. Renew. Sustain. Energy Rev. 159, 112240. doi:10.1016/j.rser.2022.112240
Smdani, G., Islam, M. R., Ahmad Yahaya, A. N., and Bin Safie, S. I. (2022). Performance Evaluation of Advanced Energy Storage Systems: A Review. Energy & Environ. 34 (4), 1094–1141. doi:10.1177/0958305x221074729
Sobol, I. M. (2001). Global Sensitivity Indices for Nonlinear Mathematical Models and Their Monte Carlo Estimates. Math. Comput. Simul. 55 (1-3), 271–280. doi:10.1016/s0378-4754(00)00270-6
Steventon, M. J., Jackson, C. A. L., Hall, M., Ireland, M. T., Munafo, M., and Roberts, K. J. (2022). Reproducibility in Subsurface Geoscience. Earth Sci. Syst. Soc. 2. doi:10.3389/esss.2022.10051
Strozyk, F. (2017). The Internal Structure of the Zechstein Salt and Related Drilling Risks in the Northern Netherlands. Geology, Environmental Science 115–128. doi:10.1016/B978-0-12-809417-4.00006-9
Sunny, N., Mac Dowell, N., and Shah, N. (2020). What Is Needed to Deliver Carbon-Neutral Heat Using Hydrogen and CCS? Energy & Environ. Sci. 13 (11), 4204–4224. doi:10.1039/d0ee02016h
Svanberg, M., Ellis, J., Lundgren, J., and Landälv, I. (2018). Renewable Methanol as a Fuel for the Shipping Industry. Renew. Sustain. Energy Rev. 94, 1217–1228. doi:10.1016/j.rser.2018.06.058
Tan, Z., Zhang, Y., Niu, J., Wenqi Ke, G. C., Zeng, H., and Liu, L. (2021). Construction Progress of Deep Underground Salt Cavern Gas Storage and Challenges of its Drilling and Completion Technology. E3S Web Conf. 329, 01043. doi:10.1051/e3sconf/202132901043
Tarkowski, R., and Czapowski, G. (2018). Salt Domes in Poland – Potential Sites for Hydrogen Storage in Caverns. Int. J. Hydrogen Energy 43 (46), 21414–21427. doi:10.1016/j.ijhydene.2018.09.212
Underground Sun Storage, E. N. (2023). Underground Sun Storage: World's First Geological Hydrogen Storage Facility Goes into Operation. Available at: https://www.uss-2030.at/en/public-relations-/-publications/press/details/article/underground-sun-storage-worlds-first-geological-hydrogen-storage-facility-goes-into-operation.html.
Walsh, S. D. C., Easton, L., Wang, C., and Feitz, A. J. (2023). Evaluating the Economic Potential for Geological Hydrogen Storage in Australia. Earth Sci. Syst. Soc. 3. doi:10.3389/esss.2023.10074
Warren, J. K. (2016). Evaporites - A Geological Compendium (2 ed). Springer Cham. doi:10.1007/978-3-319-13512-0
Williams, J. D. O., Williamson, J. P., Parkes, D., Evans, D. J., Kirk, K. L., Sunny, N., et al. (2022). Does the United Kingdom Have Sufficient Geological Storage Capacity to Support a Hydrogen Economy? Estimating the Salt Cavern Storage Potential of Bedded Halite Formations. J. Energy Storage 53, 105109. doi:10.1016/j.est.2022.105109
Yang, C., Wang, T., and Chen, H. (2023). Theoretical and Technological Challenges of Deep Underground Energy Storage in China. Engineering 25, 168–181. doi:10.1016/j.eng.2022.06.021
Zhang, G., Liu, Y., Wang, T., Zhang, H., Wang, Z., Zhao, C., et al. (2021). Pillar Stability of Salt Caverns Used for Gas Storage Considering Sedimentary Rhythm of the Interlayers. J. Energy Storage 43, 103229. doi:10.1016/j.est.2021.103229
Zhu, S., Shi, X., Yang, C., Li, Y., Li, H., Yang, K., et al. (2023). Hydrogen Loss of Salt Cavern Hydrogen Storage. Renew. Energy 218, 119267. doi:10.1016/j.renene.2023.119267
Keywords: hydrogen storage, salt caverns, geological modelling, energy systems, renewable energy
Citation: Barnett HG, Ireland MT and Van Der Land C (2024) Capturing Geological Uncertainty in Salt Cavern Developments for Hydrogen Storage. Earth Sci. Syst. Soc. 4:10125. doi: 10.3389/esss.2024.10125
Received: 28 March 2024; Accepted: 16 October 2024;
Published: 08 November 2024.
Edited by:
Davide Gamboa, University of Aveiro, PortugalCopyright © 2024 Barnett, Ireland and Van Der Land. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hector G. Barnett, aC5iYXJuZXR0MkBuY2wuYWMudWs=
 Hector G. Barnett
Hector G. Barnett Mark Thomas Ireland
Mark Thomas Ireland Cees Van Der Land
Cees Van Der Land